Unsteady Magnetohydrodynamics (MHD) Natural Convective Flow of Nanofluids Over an Infinite Perpendicular Absorbent Plate
←
→
Page content transcription
If your browser does not render page correctly, please read the page content below
Copyright © 2023 by American Scientific Publishers Journal of Nanofluids
All rights reserved. Vol. 12, pp. 280–287, 2023
Printed in the United States of America (www.aspbs.com/jon)
Unsteady Magnetohydrodynamics (MHD) Natural
Convective Flow of Nanofluids Over an Infinite
Perpendicular Absorbent Plate
Ch. H. K. Gopal∗ , M. Sudhakar, and S. Masthan Rao
Department of Mathematics and Humanities, RVR & JC College of Engineering, Chowdavaram, Guntur 522019,
Andhra Pradesh, India
The magnetic fields played the significant roles in plentiful field they are, biologically, chemically, mechanically
as well as medically all investigations. In clinical as well as medical investigation the magnets were extremely
imperative to create 3-dimensional images of anatomical as well as diagnostics significance from nuclear mag-
netic resonances signal. In views of those applications, the purpose of present research is to the unsteady
MHD convective flow past a moving vertical porous plate in nanofluids in the presence of a uniform transverse
magnetic field has been carried out. The governing equations are solved using Laplace transform technique
and the solutions are presented in closed form. The numerical computations of velocity and nanofluid temper-
ature the rate of heat transfer and the shear stress at the plate are presented graphically for several values
ARTICLE
of the pertinent parameters. An increase in radiation parameter leads to decrease the fluid velocity as well as
temperature in the boundary layer region. The velocity enhances with increasing permeability parameter. An
increase in Grashof number and an increase in time lead to increase the fluid temperature. The rate of heat
transfer at the plate is found to be higher for Cu-water nanofluid. The shear stress at the plate for Cu-water
IP: 5.10.31.151 On: Thu, 11 May 2023 10:35:21
nanofluid is found to be lower. TheCopyright:
present study has many
American applications
Scientific in engineering devices.
Publishers
Delivered by Ingenta
KEYWORDS: Natural Convection, MHD Flows, Nanofluid, Thermal Radiation, Vertical Plate.
1. INTRODUCTION Emery.1 Rajesh et al.2 researched the consequences of ther-
Nanoscale particles less than 100 nm have been devel- mal radiation and chemical reaction in the existence of
oped through nanotechnology-based procedures. The ther- Newtonian heating on the transient MHD natural convec-
mal properties of the base fluid can be enhanced with tive fluid. Rajesh and Varma3 explored radiation and mass
nanoparticles to form the stable suspension. The addi- exchange impacts on MHD natural convective stream past
tion of small amounts of nanoparticles in metal or metal an exponentially accelerated vertical plate with mutable
oxide to fluid has been shown to enhance its thermal temperature. Chamkha et al.4 built up a model utilized
conductivity. Corresponding to existing working fluids, for the nanofluid consolidates the impacts of Brownian
nanofluids offer much heat absorbing and heat trans- movement and thermophoresis with the Roseland dissem-
fer properties. Due to its extraordinary applications in ination estimate. Samad and Rahman5 discussed the inter-
electronics, communication, and computational systems, action of thermal radiation with an unsteady MHD flow
optical devices, etc. research in nanofluids has attracted through a permeable plate by presenting a time-dependent
considerable interest in recent years. The wide-ranging suction. Hamad,6 Krishna et al.,7 Kataria and Mittal,8
application in physics and engineering especially in the and Chamkha and Aly9 discussed the unsteady MHD
design of components and equipment, space technology convective flows through porous medium in different phys-
and gas turbines, etc. thermal radiation on natural con- ical configurations. Material processing in which mag-
vection has become extremely relevant. For absorbing netic fields are known for their magnificent control of
and non-absorbing gases, the impact of thermal radiation electrically-conducting materials is carried discussed the
on a laminar, Natural convective boundary layer which role of a magnetic field on the unsteady natural convec-
flows along a vertical plate was examined by England and tive nanofluid which stream over a vertical plate. Sheik-
holeslami et al.10 examined the heat transfer of Cu–H2 O
∗
nanofluid in presence of a magnetic field by considering
Author to whom correspondence should be addressed.
Email: krishnagopalch@gmail.com the effect of Brownian motion. The motivation behind all
Received: 5 December 2021 the above-presented research considers made on nanoflu-
Accepted: 10 February 2022 ids, was to comprehend and take advantage of nanofluids
280 J. Nanofluids 2023, Vol. 12, No. 1 2169-432X/2023/12/280/008 doi:10.1166/jon.2023.1928Gopal et al. Unsteady MHD Natural Convective Flow of Nanofluids Over an Infinite Perpendicular Absorbent Plate
heat transfer mechanism. The viscous dissipation impact and Chamkha.35 Krishna et al.36 discussed the MHD flow
is also significantly affecting the heat transfer mechanism. of an electrically conducting second-grade fluid through
The distribution of the temperature in the boundary layer porous medium over a semi-infinite vertical stretching
is greatly influenced by the viscous dissipation as an inter- sheet. Krishna et al.37 discussed Hall effects on MHD peri-
nal source of heat-induced by fluid shearing. Khan et al.,11 staltic flow of Jeffrey fluid through porous medium in a
Freidoonimehr et al.,12 and Mustafa et al.13 analysed the vertical stratum. Krishna et al.38 discussed heat and mass-
influence of unsteady MHD natural convective boundary transfer effects on an unsteady flow of a chemically react-
layer nanofluid along with a stretching sheet with vis- ing micropolar fluid over an infinite vertical porous plate
cous dissipation. The influence on MHD nanofluid flow in the presence of an inclined magnetic field, Hall cur-
of a wedge with permeable slip and the medium was rent effect, and thermal radiation taken into account. The
investigated by Pandey and Kumar14 and Upreti et al.15 effects of heat and mass transfer on free convective flow of
Rajesh et al.16 established a numerical model for Tran- micropolar fluid over an infinite vertical porous plate have
sient MHD nanofluid to understand the characteristics of been discussed by Krishna et al.39 Krishna and Chamkha40
heat transfer in the existence of viscous dissipation. Mishra have discussed the systematic solution of time-dependent
et al.17 analysed the impact of Ohmic-viscous dissipation mean velocity on MHD peristaltic rotating flow of an elec-
and slip effects on nanofluid flow over a stretching cylin- trically conducting couple stress fluid in a uniform elas-
der with suction/injection. Motsumi and Makinde18 stud- tic porous channel. Krishna and Chamkha41 investigated
ied the impact of thermal radiation and viscous dissipation the Hall and ion slip effects on the MHD convective flow
on boundary layer flow of nanofluids over a permeable of elastico-viscous fluid through porous medium between
moving flat plate. Haroun et al.19 examined the unsteady two rigidly rotating parallel plates with time fluctuating
MHD mixed convection in a nanofluid due to a stretching/ sinusoidal pressure gradient. Krishna et al.42 discussed the
shrinking surface with suction/injection using the spec- Soret and Joule effects of MHD mixed convective flow of
ARTICLE
tral relaxation method. Farooq et al.20 discussed the influ- an incompressible and electrically conducting viscous fluid
ence of transpiration and viscous dissipation on entropy past an infinite vertical porous plate taking Hall effects into
flow over a nonlinear radially stretching disk. Kuznetsov account. Krishna et al.43 discussed the heat and mass trans-
21
and Nield have studied the natural convective boundary fer on unsteady, MHD oscillatory flow of second-grade
IP: 5.10.31.151 On: Thu, 11 May 2023 10:35:21
layer flow of a nanofluid past a vertical plate. Hamad and fluid through
Copyright: American Scientific a porous medium. Krishna et al.44 investi-
Publishers
22
Pop have investigated the unsteady MHD freeDelivered convec- bygated the heat and mass transfer on MHD free convective
Ingenta
tion flow of a nanofluid past a vertical permeable flat plate flow over an infinite non-conducting vertical flat porous
in a rotating frame of reference with constant heat source. plate.
The effects of magnetic field on free convection flow of a Chamkha and Khaled45 discussed the problem of cou-
nanofluid past a vertical semi-infinite flat plate were stud- pled heat and mass transfer by mixed convection in a lin-
ied by Hamad et al.23 Turkyilmazoglu24 has obtained an early stratified stagnation flow with an externally applied
analytical solution for heat and mass transfer of MHD slip magnetic field and internal heat generation or absorp-
flow in nanofluids. Nandkeolyar et al.25 have presented the tion effects. Chamkha et al.46 investigated coupled heat
unsteady hydromagnetic radiative flow of a nanofluid past and mass transfer by boundary-layer free convection over
a flat plate with ramped temperature. a vertical flat plate. The free convection boundary-layer
Krishna and Chamkha31 investigated the diffusion- flow over an isothermal inclined plate embedded in a
thermo, radiation-absorption and Hall and ion slip effects thermally stratified porous medium has been developed
on MHD free convective rotating flow of nano-fluids by Chamkha.47 Reddy and Chamkha48 discussed Soret
past a semi-infinite permeable moving plate with constant and Dufour effects on MHD convective flow of Al2 O3 -
heat source. Krishna and Chamkha32 discussed the MHD Water and TiO2 -Water nanofluids past a stretching sheet in
squeezing flow of a water-based nanofluid through a sat- porous media. The steady, laminar, MHD flow of a microp-
urated porous medium between two parallel disks, taking olar fluid past a stretched semi-infinite, vertical and per-
the Hall current into account. Hall and ion slip effects meable has been explored by Khedr et al.49 Takhar et al.50
on unsteady MHD convective rotating flow of nanoflu- investigated the unsteady flow and heat transfer on a semi-
ids have been discussed by Krishna and Chamkha.33 The infinite flat plate with an aligned magnetic field. A study
effects of radiation and Hall current on an unsteady MHD of natural convective flow, heat transfer and entropy gener-
free convective flow in a vertical channel filled with a ation in an odd-shaped geometry has presented by Parvin
porous medium have been studied by Krishna et al.34 and Chamkha.51 The effects of nanoparticles diameter and
The heat generation/absorption and thermo-diffusion on concentration on natural convection heat transfer of a
an unsteady free convective MHD flow of radiating and nanofluid around a vertical cone embedded in a Darcy
chemically reactive second grade fluid near an infinite porous medium utilizing the drift-flux model have been
vertical plate through a porous medium and taking the theoretically investigated Ghalambaz et al.52 Zaraki et al.53
Hall current into account have been studied by Krishna theoretically explored the problem of natural convection
J. Nanofluids, 12, 280–287, 2023 281Unsteady MHD Natural Convective Flow of Nanofluids Over an Infinite Perpendicular Absorbent Plate Gopal et al.
boundary layer heat transfer of nanofluids. The effects of Table I. Thermophysical properties of H2 O, Cu and Ag.
Joule-heating, chemical reaction and thermal radiation on
H2 O Cu Ag
unsteady MHD natural convection from a heated vertical
porous plate in a micropolar fluid have been analyzed by cp (J/Kg K) 4179 385 235
Chamkha et al.54 (Kg/m3 ) 997.1 8933 10500
k (W/m K) 0.613 401 429
The purpose of this analysis is to investigate the impacts × 10−5 (1/K) 21 1.67 1.89
of radiation and magnetic field on a transient natural (S/m) 5.5 × 10−6 59.6 × 106 62.1 × 106
free convective nanofluid that stream along with a verti-
cal plate. In this paper, the MHD convective flow past a
moving vertical porous plate in nanofluids with the pres- motion. This approximation is exact enough for both drop-
ence of a uniform transverse magnetic field has been dis- ping fluids and gases at small values of the temperature
cussed. With the aid of non-dimensional flow parameters, difference. As the plate is infinitely long, the velocity and
the mathematical results of velocity and temperature dis- temperature fields are functions of y and t alone. The
tributions are analysed and shown diagrammatically. This thermophysical properties of the nanofluids are given in
analysis also highlights the consistency of the numerical Table I.
approach using grid independence that is presented in the It is assumed that induced magnetic field produced by
tables. the fluid motion is negligible in comparison with the
applied one so that we consider magnetic field B = (0,
2. FORMULATION AND SOLUTION OF THE 0, B0 ). This assumption is justified, since the magnetic
PROBLEM Reynolds number is very small for metallic liquids and
partially ionized fluids. Also, no external electric field is
We considered the radiation-absorption on the unsteady
applied such that the effect of polarization of fluid is neg-
MHD free convective flow of a nanofluid past an infinite
ligible, so we assume E = (0, 0, 0). Under the above
ARTICLE
vertical flat plate moving with an impulsive motion. Ini-
assumptions, the momentum and energy equations in the
tially the plate is at rest with the ambient temperature T .
At time t > 0, the plate starts to move in its own plane with presence of magnetic field and thermal radiation past a
the velocity u0 in the vertical direction, where u0 is con- moving vertical plate can be expressed as (Krishna and
IP: 5.10.31.151 On: Thu, 11 May 2023
Chamkha 28 10:35:21
and Das and Jana27 ),
stant and the temperature of the plate Copyright:
is raised or American
lowered Scientific Publishers
to Tw . We choose the x-axis along the plate in theDelivered
vertical by Ingenta
u 2 u f
direction and y-axis perpendicular to the plate. A uniform nf = nf 2 − nf B02 u − u + g nf T − T (1)
t y k
transverse magnetic field of strength B0 is applied parallel
to the y-axis. The plate coincides with the plane y = 0 and T 2 T q
the flow being confined to y > 0. The physical model of cp nf = knf 2 − r + Q1 C − C (2)
t y y
the problem is as shown in the Figure 1.
C 2 C
The assumptions of the present problem are made as =D 2 (3)
the following. The pressure gradient is neglected in this t y
problem. A radiative heat flux qr is applied in the normal The important attributes of nanofluid are,
direction to the plate. The fluid is a water based nanofluid f
containing two types of nanoparticles Cu and Ag. The nf = = 1 − f + s
base fluid and the suspended nanoparticles are in thermal 1 − 2 5 nf
equilibrium. The density is assumed to be linearly depen- cp nf = 1 − cp f + cp s
dent on temperature buoyancy forces in the equations of
nf = 1 − f + s
3 − 1
nf = f 1 + = s
+ 2 − − 1 f
(4)
the effective thermal conductivity of the nanofluid29 30
given by
ks + 2kf − 2 kf − ks
knf = kf (5)
ks + 2kf + kf − ks
The initial and boundary conditions be
Fig. 1. Physical model. u=0 T =T C = C at t =0 for all y ≥ 0
282 J. Nanofluids, 12, 280–287, 2023Gopal et al. Unsteady MHD Natural Convective Flow of Nanofluids Over an Infinite Perpendicular Absorbent Plate
u = u0 T =Tw C =Cw at t > 0 y=0 To solve the Eqs. (11)–(13) with initial and bound-
ary conditions (14) by making use of Laplace transform
u→0 T → T C → C t > 0 as y →
technique.
(6)
Taking Laplace transforms on Eqs. (11)–(13), then the
The Rosseland approximation26 applies to optically transformed equations are,
thick media and gives the net radiation heat flux qr through
2 u 1
the expression as, a1 2 − s M + 2
a3 u + Gr a2 = 0 (15)
K
4 ∗ T 4
qr = − (7) 2
3K ∗ y a4 − s + Q = 0 (16)
2
It is supposed that, the temperature difference T − T
d2
within the boundary layer flow is sufficiently small such − sSc = 0 (17)
that the term T 4 may be expressed as a linear function d 2
of temperature. This is done by expanding T 4 in a Taylor The relevant boundary conditions for ū, ¯ and ¯ are
series about a free stream temperature T , as pursues,
1 1
u= = = at =0
T 4 = T4 + 3T3 T − T + 6T2 T − T 2 + · · · (8) s s s
Neglecting higher order terms in Eq. (8) ahead of the u→0 →0 →0 as → (18)
first order in (T − T ), we acquired, Where,
T ≈
4
4T3 T − 3T4 (9)
ū s = u t e−st dt
ARTICLE
0
On the utilize of Eqs. (7) and (9), Eq. (2) turns into,
2 ¯
s = t e−st dt
∗ 3
T 1 16 T T 0
= knf + + Q1 C − C (10)
t cp nf 3k∗ y 2 ¯
IP: 5.10.31.151 On: Thu, 11 May 2023 10:35:21 s = t e−st dt
0
Implementing non-dimensional quantities, Copyright: American Scientific Publishers
Delivered by Ingenta
Transformed solutions of Eqs. (15)–(17) put through the
u0 y ∗
2
u0 t ∗ u T − T boundary requirements (18) are obtained and are provided
= t = u = =
vf vf u0 Tw − T as,
1 − √sSc
C − C 2
f B0 vf ∗
16 T 3 s = e (19)
= M2 = Nr = s
Cw − C f u0 2
3kf k∗ 1 Q √ Q 1 − √sSc
s = + e− s + e (20)
f cp gf vf Tw − T ku20 s Sc − Sc − s 2
Pr = Gr = K= 2
kf u30 vf
b1 b
v vf Q1 Cw − C u s = + + 2 2
Sc = Q= s ss − 1 s s − 1
D u20 Tw − T √
b b1 √
+ 2 3 e− s+ /a1 − e− s
Making use of non-dimensional variables, the governing s s −2 ss −1
Eqs. (2), (3) and (10) reduced to (dropping asterisks), b2 √ b3 √
− s − sSc
− e − e (21)
u 2 u 1 s 2 s − 1 s 2 s − 2
= a1 2 − M 2 + a3 u + Gr a2 (11)
t K Taking inverse Laplace transforms of Eqs. (19)–(21),
2
then, we acquired the solutions for the concentration, tem-
= a4 2 + Q (12) perature and velocity fields.
t
The shear stress at the surface = 0 measured as,
1 2
= (13) u
t Sc 2 = (22)
The initial and boundary conditions are, =0
The Nusselt number in terms of rate of heat transfer at
u = 0 = 0 t = 0 for all ≥0
the plate = 0 is given by
u = = 1 = 1 t > 0 at =0
u → 0 → 0 → 0 t > 0 as → (14) Nu = (23)
=0
J. Nanofluids, 12, 280–287, 2023 283Unsteady MHD Natural Convective Flow of Nanofluids Over an Infinite Perpendicular Absorbent Plate Gopal et al.
The Sherwood number in terms of rate of mass transfer
at the plate = 0 is given by
Sh = (24)
=0
3. RESULTS AND DISCUSSION
In order to get a clear insight on the physics of the prob-
lem, a parametric study is performed and the obtained
numerical results are elucidated with the help of graphical
illustrations. We have presented the non-dimensional fluid
velocity u and the fluid temperature for several values
of magnetic parameter M 2 , Grashof number Gr, radiation
parameter Nr, volume fraction parameter and time s in Fig. 3. The velocity profile with K. M = 2, Nr = 0.5, = 0.05, Gr = 3,
Figures 2–11. The values of volume fraction of nanoparti- t = 0.1.
cles are taken in the range of 0 ≤ ≤ 0 2. The case M = 0
corresponds to the absence of magnetic field and = 0 for
regular fluid. The default values of the other parameters
are mentioned in the description of the respected figures.
We consider the non-dimensional velocity distribution for
nanoparticle (Cu). Due to high density of Cu, for Cu-water
the dynamic viscosity increases more and leads to a thin-
ARTICLE
ner boundary layer than other particles. For the cases of
stationary plate ( = 0) as well as moving plate ( = 1).
Figure 2 reveals that the fluid velocity u deccelerates for
increasing values of magnetic parameter M. The momen-
IP: 5.10.31.151 On: Thu, 11 May 2023 10:35:21
tum boundary layer thickness decreases Copyright: American
for increasing val- Scientific Publishers
ues of M for the cases of stationary plate ( = 0)Delivered
as well by Ingenta
as moving plate ( = 1). The velocity profiles are char-
acterized by distinctive peaks in the immediate vicinity
of the plate and as M increases these peaks decrease and Fig. 4. The velocity profile with Nr. M = 2, K = 0.5, = 0.05, Gr = 3,
t = 0.1.
move gradually downstream. This is due to the fact that
the magnetic lines of forces move past the plate and the
fluid which is decelerated by the viscous force, receives lesser the fluid speed is observed in the entire fluid region.
a push from the magnetic field which counteracts the vis- The effect of radiation parameter Nr on the velocity pro-
cous effects. files is presented in Figure 4. The fluid velocity u enhances
Figure 3 depicts that the velocity increases with increas- as the value of Nr increases for both cases of stationary
ing permeability parameter K. Lower the permeability plate ( = 0) as well as moving plate ( = 1). The velocity
Fig. 2. The velocity profile with M. K = 0.5, Nr = 0.5, = 0.05, Gr = Fig. 5. The velocity profile with . M = 2, K = 0.5, Nr = 0.5, Gr = 3,
3, t = 0.1. t = 0.1.
284 J. Nanofluids, 12, 280–287, 2023Gopal et al. Unsteady MHD Natural Convective Flow of Nanofluids Over an Infinite Perpendicular Absorbent Plate
Fig. 6. The velocity profile with Gr. M = 2, K = 0.5, Nr = 0.5, = Fig. 9. The temperature profile with Nr. Pr = 0.71, = 0.05, t = 0.1.
0.05, t = 0.1.
ARTICLE
IP: 5.10.31.151 On: Thu, 11 May 2023 10:35:21
Copyright: American Scientific Publishers
Delivered by Ingenta
Fig. 10. The temperature profile with . Pr = 0.71, Nr = 0.5, t = 0.1.
Fig. 7. The velocity profile with M. M = 2, K = 0.5, Nr = 0.5, =
0.05, Gr = 3. tends to increase inside a boundary layer region. Figure 5
depicts the effect of solid volume fraction of nanoparti-
profiles increase sharply near the surface of the plate cles on the fluid velocity. The fluid velocity u increases
and after attaining respective maxima’s, the curves settle with increasing for the cases of stationary plate ( = 0)
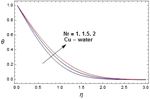
down to the corresponding asymptotic value. Therefore, Nr as well as moving plate ( = 1). It is also revealed that
behaves like a supporting force which accelerates the fluid the increase in the values of results in the increase of
particles near the vicinity of the plate. Also, it is noted that the momentum boundary layer thickness. Figure 6 shows
momentum boundary layer thickness increases when Nr that the velocity u increases with an increase in Grashof
Fig. 8. The temperature profile with Pr. Nr = 0.5, = 0.05, t = 0.1. Fig. 11. The temperature profile with Pr. Pr = 0.71, Nr = 0.5, = 0.05.
J. Nanofluids, 12, 280–287, 2023 285Unsteady MHD Natural Convective Flow of Nanofluids Over an Infinite Perpendicular Absorbent Plate Gopal et al.
number Gr for the cases of stationary plate ( = 0) as Table III. Nusselt number.
well as moving plate ( = 1). This trend is due to the
Pr Nr t Nu
fact that the positive Grashof number Gr acts like a favor-
able pressure gradient which accelerates the fluid in the 0.71 1 0.05 0.1 −1.01909
boundary layer. Consequently, the velocity increases with 3 −2.09480
7 −3.19985
Gr. Grashof number represents the effect of free convec- 1.5 −0.91821
tion currents. Physically, Gr > 0 means heating of the fluid 2 −0.84237
of cooling of the boundary surface, Gr < 0 means cool- 0.2 −0.89126
ing of the fluid of heating of the boundary surface and 0.4 −0.72632
Gr = 0 corresponds the absence of free convection current. 0.2 −0.72060
0.3 −0.58837
Figure 7 reveals that the fluid velocity u increases as time
s increases for both cases of stationary plate ( = 0) as
well as moving plate ( = 1).
Table IV. Comparison of the results (y = 0.2, = 0).
Figure 8 represents the variation of nanofluid tem-
perature for Prandtl number Pr. The temperature pro- Previous work Present results
files exhibit that the fluid temperature decreases as Pr M K Nr Das and Jana27 K→
increases. This is due to the fact that a higher Prandtl num- 2 0.5 1 0.05 0.522142 0.522145
ber fluid has relatively low thermal conductivity, which 3 0.458448 0.458496
reduces conduction and there by the thermal boundary 4 0.355487 0.355447
layer thickness; and as a result, temperature decreases. 1 0.565894 0.565852
1.5 0.605221 0.605241
From Figure 9, an increase in radiation parameter Nr
1.5 0.587447 0.587463
means the release of heat energy from the flow region and 2 0.622465 0.622447
so the fluid temperature decreases. This means that, the
ARTICLE
0.2 0.597995 0.597996
thermal boundary layer decreases and more uniform tem- 0.4 0.650632 0.650621
perature distribution across the boundary layer. Figure 10
displays the effect of volume fraction of nanoparti-
cles on the temperature distribution.IP:The
5.10.31.151 On: Thu, 11
fluid temperature May 2023 10:35:21
asymptotically to the free stream with zero value far away
Copyright: American
increases as volume fraction parameter enlarges. Also, Scientific
from the Publishers
plate.
Delivered by Ingenta
the thermal boundary layer for Cu-water is greater than The shear stress at the plate and Nusselt number in
for pure water ( = 0). This is because copper has high terms of rate of heat transfer are determined analytically
thermal conductivity and its addition to the water based and computationally discussed with reference to governing
fluid increases the thermal conductivity for the fluid, so the parameters and are tabulated in Tables II and III. The stress
thickness of the thermal boundary layer increases. It is also component reduces with increasing permeability parame-
observed that with increasing the volume fraction of the ter K with increasing radiation parameter Nr, nano particle
nanoparticles the thermal boundary layer is increased. This concentration and enhances with increasing Hartmann
agrees with the physical behavior of nanoparticles. This number, thermal Grashof number Gr and time t.
observation shows that the use of nanofluids will be sig- Nusselt number reduces with Prandtl number Pr and
nificance in the cooling and heating processes. Figure 11 accelerates with increasing radiation parameter Nr, nano
reveals that temperature increases with increasing time s. particle concentration and time t. Since the thermal con-
The fluid temperature is high near the plate and decreases ductivity of Cu is higher than other nano fluids, the rate of
heat transfer is found to be higher for Cu-water nanofluid.
Table II. Shear stress. Also due to increase in thermal conductivity with the solid
volume fraction of nanoparticles. Also, the thermal bound-
M K Nr Gr t x
ary layer thickness decreases with increase of nanoparti-
2 0.5 1 0.05 3 0.2 0.510052 cle volume fraction and in turn the rate of heat transfer
3 2.983180 increases with increase of volume fraction of nanoparti-
4 4.218522
1 0.407968
cles. The results are good agreement with results of Das
1.5 0.333386 and Jana27 (Table IV).
1.5 0.409731
2 0.373085
0.2 0.501324 4. CONCLUSIONS
0.4 0.483255 To obtain exact solutions for the unsteady natural convec-
4 1.655895 tion boundary layer flow of a nanofluid near a moving infi-
5 2.114558
nite vertical plate in the presence of a transverse uniform
0.3 0.652554
0.4 0.854478 magnetic field. The most important concluding remarks
can be summarized as follows.
286 J. Nanofluids, 12, 280–287, 2023Gopal et al. Unsteady MHD Natural Convective Flow of Nanofluids Over an Infinite Perpendicular Absorbent Plate
(1) An increase in radiation parameter leads to decrease 26. S. Rosseland, Astrophysik und Atom-Theoretische Grundlagen,
the fluid velocity as well as temperature in the boundary Springer-Verlag, Berlin (1931).
layer region. 27. S. Das and R. N. Jana, Alexandria Engineering Journal 54, 55
(2015).
(2) The velocity enhances with increasing permeability 28. M. V. Krishna and A. J. Chamkha, Results Phys. 15, 102652 (2019).
parameter. 29. S. Kakac and A. Pramuanjaroenkij, Int. J. Heat Mass Transf. 52,
(3) An increase in Grashof number and an increase in 3187 (2009).
time lead to increase the fluid velocity and temperature. 30. H. F. Oztop and E. Abu-Nada, Int. J. Heat Fluid Flow 29, 1326
(4) The rate of heat transfer at the plate is found to be (2008).
31. M. V. Krishna and A. J. Chamkha, Results in Physics 15, 102652
higher for Cu-water nanofluid. (2019).
(5) The shear stress at the plate for Cu-water nanofluid is 32. M. V. Krishna and A. J. Chamkha, Journal of Porous Media 22, 209
found to be lower. (2019).
33. M. V. Krishna and A. J. Chamkha, Journal of Egyptian Mathemati-
cal Society 28, 1 (2020).
34. M. V. Krishna, G. S. Reddy, and A. J. Chamkha, Physics of Fluids
References and Notes 30, 23106 (2018).
1. W. England and A. Emery, J. Heat Transfer 91, 37 (1969). 35. M. V. Krishna and A. J. Chamkha, Physics of Fluids 30, 053101
2. V. Rajesh, A. J. Chamkha, D. Bhanumathi, and S. V. K. Verma, (2018).
Comput. Therm. Sci.: Int. J. 5, 355 (2013). 36. M. V. Krishna, K. Jyothi, and A. J. Chamkha, Journal of Porous
3. V. Rajesh and S. V. K. Varma, ARPN Journal of Engineering and Media 23, 751 (2020).
Applied Sciences 4, 20 (2009). 37. M. V. Krishna, K. Bharathi, and A. J. Chamkha, Interfacial Phe-
4. A. J. Chamkha, S. Abbasbandy, A. M. Rashad, and K. Vajravelu, nomena and Heat Transfer 6, 253 (2019).
Meccanica 48, 275 (2013). 38. M. V. Krishna, B. V. Swarnalathamma, and A. J. Chamkha, Special
5. M. A. Samad and M. M. Rahman, J. Nav. Architect. Mar. Eng. 3, 7 Topics and Reviews in Porous Media—An International Journal 9,
(2006). 347 (2018).
6. M. Hamad, Int. Commun. Heat Mass Tran. 38, 487 (2011). 39. M. V. Krishna, P. V. S. Anand, and A. J. Chamkha, Special Topics
ARTICLE
7. P. M. Krishna, V. Sugunamma, and N. Sandeep, Chem. Process Eng. and Reviews in Porous Media—An International Journal 10, 203
Res. 25, 39 (2014). (2019).
8. H. R. Kataria and A. S. Mittal, Appl. Therm. Eng. 110, 864 (2017). 40. M. V. Krishna and A. J. Chamkha, Special Topics and Reviews in
9. A. J. Chamkha and A. Aly, Chem. Eng. Commun. 198, 425 (2010). Porous Media: An International Journal 10, 245 (2019).
10. M. Sheikholeslami, M. G. Badpy, D. D.IP: 5.10.31.151
Ganji, and S. Soheil, On: Thu, 11
Journal 41. May
M. V. 2023
Krishna10:35:21
and A. J. Chamkha, International Communications in
Copyright:
of the Taiwan Institute of Chemical Engineers American Scientific
45, 40 (2014). Publishers
Heat and Mass Transfer 113, 104494 (2020).
11. M. S. Khan, I. Karim, L. E. Ali, and A. Islam, Int. Nano Delivered
Lett. 2, 24 by42.
Ingenta
M. V. Krishna, B. V. Swarnalathamma, and A. J. Chamkha, Journal
(2012). of Ocean Engineering and Science 4, 263 (2019).
12. N. Freidoonimehr, M. M. Rashidi, and S. Mahmud, Int. J. Therm. 43. M. V. Krishna, K. Jyothi, and A. J. Chamkha, Int. Jour. of Fluid
Sci. 87, 136 (2015). Mech. Res. 45, 459 (2018).
13. M. Mustafa, A. Mushtaq, T. Hayat, and B. Ahmed, PloS One 9, 44. M. V. Krishna, M. G. Reddy, and A. J. Chamkha, Int. Jour. of Fluid
e103946 (2014). Mech. Res. 46, 1 (2019).
14. A. K. Pandey and M. Kumar, Alexandria Engineering Journal 55, 45. A. J. Chamkha and A. R. A. Khaled, International Journal of
3115 (2016). Numerical Methods for Heat and Fluid Flow 10, 94 (2000).
15. H. Upreti, A. K. Pandey, and M. Kumar, Alexandria Engineering 46. A. J. Chamkha, A. F. Al-Mudhaf, and I. Pop, International Commu-
Journal 57, 1839 (2018). nications in Heat and Mass Transfer 33, 1096 (2006).
16. V. Rajesh, M. Mallesh, and O. A. Beg, Procedia Materials Science 47. A. J. Chamkha, International Journal of Engineering Science 35,
10, 80 (2015). 975 (1997).
17. A. Mishra, A. K. Pandey, and M. Kumar, Nanoscience and Technol- 48. P. S. Reddy and A. J. Chamkha, Adv. Powder Technol. 27, 1207
ogy: Int. J. 9, 99 (2018). (2016).
18. T. Motsumi and O. Makinde, Phys. Scripta 86, 045003 (2012). 49. M. E. M. Khedr, A. J. Chamkha, and M. Bayomi, Nonlinear Anal-
19. N. A. Haroun, P. Sibanda, S. Mondal, and S. S. Motsa, Bound. Value ysis: Modelling and Control 14, 27 (2009).
Probl. 24, 1 (2015). 50. H. S. Takhar, A. J. Chamkha, and G. Nath, International Journal of
20. U. Farooq, M. I. Afridi, M. Qasim, and D. C. Lu, Entropy 20, 668 Engineering Science 37, 1723 (1999).
(2018). 51. S. Parvin and A. J. Chamkha, International Communications in Heat
21. A. V. Kuznetsov and D. A. Nield, Int. J. Therm. Sci. 49, 243 (2010). and Mass Transfer 54, 8 (2014).
22. M. A. A. Hamad and I. Pop, Heat Mass Transfer. 47, 1517 (2011). 52. M. Ghalambaz, A. Behseresht, J. Behseresht, and A. J. Chamkha,
23. M. A. A. Hamad, I. Pop, and I. A. M. Ismail, Nonlinear Anal. Real Adv. Powder Technol. 26, 224 (2015).
World Appl. 12, 1338 (2011). 53. A. Zaraki, M. Ghalambaz, A. J. Chamkha, M. Ghalambaz, and D. D.
24. M. Turkyilmazoglu, Chem. Eng. Sci. 84, 182 (2014). Rossi, Adv. Powder Technol. 26, 935 (2015).
25. R. Nandkeolyar, M. Das, and H. Pattnayak, J. Orissa Math. Soc. 32, 54. A. J. Chamkha, R. A. Mohamed, and S. E. Ahmed, Meccanica 46,
15 (2013). 399 (2011).
J. Nanofluids, 12, 280–287, 2023 287You can also read