Evaluation of the applicability of different viscoelasticity constitutive models in bamboo scrimber short-term tensile creep property research
←
→
Page content transcription
If your browser does not render page correctly, please read the page content below
Science and Engineering of Composite Materials 2021; 28: 363–371
Research Article
Sun Songsong and Wan Maosong*
Evaluation of the applicability of different
viscoelasticity constitutive models in bamboo
scrimber short-term tensile creep property
research
https://doi.org/10.1515/SECM-2021-0034 the modern industry [2–4]. Thus, the correct determina-
received January 19, 2021; accepted June 02, 2021 tion of the mechanical properties of this material becomes
Abstract: Bamboo scrimber is a new natural fiber-rein- important during the design stage.
forced composite material in modern industry. In this To solve this problem, creative work has been con-
paper, the tensile creep characteristics of this material ducted in recent years. For example, He Wen investigated
were chosen as the object of the study. First, axial tensile the mechanical performance of bamboo scrimber made
fracture experiments were conducted on different test spe- from a given type of moso bamboo and treated it with hot
cimens to determine the corresponding strength data. oil [5]. Naresworo Nugroho chose zephyr strands from
Then six sets of standard tensile creep experiments were another type of moso bamboo to make a structural com-
conducted under different given stress levels. Finally, the posite board [6,7]. Huang et al. examined how the acceler-
Maxwell constitutive model was applied in fitting the rela- ated aging method and aging resistance influence the
tionship between strain and time. The results showed that performance of bamboo scrimber and conducted mechanic
the traditional Maxwell viscoelasticity constitutive model experiments on a double cantilever beam and an end-
will result in some errors in the fitting results, while the notched beam [8–10]. Li and Wei conducted an experi-
combined fractional and Maxwell model can provide much mental study on the deformation and failure mechanism
higher accuracy in this study, thus it is more suitable for of bamboo scrimber and proposed an axial stress–strain
engineering applications. This paper provides a solid foun- model [11–13]. According to previous research, a primary
dation for a better understanding of the mechanism of the conclusion can be proposed that bamboo scrimber is a
bamboo scrimber creep behavior. typical kind of plywood. According to the theory of visco-
elastic mechanics, this kind of material always shows obvious
Keywords: bamboo scrimber, fractional derivative, ten- creep characteristic, which has an obvious impact on the
sile creep, viscoelasticity constitutive model service life [14–16]. While in a previous study, this material
is usually considered to be an anisotropic elastic material,
special creep property research of the bamboo material
experimental results has rarely been discovered in the pub-
1 Introduction lished documents.
In this paper, axial tensile fracture experiments were
Bamboo scrimber is a new natural fiber-reinforced com- conducted on different test specimens to determine the
posite material that has been developed in recent dec- corresponding strength data. Then six sets of standard
ades [1]. This material has several advantages (e.g., low tensile creep experiments were conducted under different
cost, green, clean, and low weight) that make it usable in given stress levels. Finally, the Maxwell viscoelasticity
constitutive model was applied in fitting the relationship
between the strain and serving time. The results showed
* Corresponding author: Wan Maosong, Vehicle Engineering, that the traditional Maxwell viscoelasticity constitutive
College of Automobile and Traffic Engineering, Nanjing Forestry
model will result in some errors in the fitting results,
University, Nanjing, 210037, China, e-mail: 513194484@qq.com
Sun Songsong: Vehicle Engineering, College of Automobile and
while the combined fractional and Maxwell model can
Traffic Engineering, Nanjing Forestry University, Nanjing, 210037, provide much higher accuracy in this study, and thus is
China more suitable for engineering applications.
Open Access. © 2021 Sun Songsong and Wan Maosong, published by De Gruyter. This work is licensed under the Creative Commons
Attribution 4.0 International License.364 Sun Songsong and Wan Maosong
2 Method
In the present short-term creep experiments of the fiber-
reinforced composites, the load applied on the specimen
is always determined by the limit strength of the material
(usually the range is no more than 70%). According
to a previous study, some of the mechanical property
parameters of the bamboo scrimber such as the tensile
strength or young’s modulus always show obvious dis-
persion. As a result of this, it is necessary to conduct a
statistical analysis to obtain the distribution property of
the tensile strength before the creep experiment. So the
whole process of the research can be divided into five
steps:
Step 1: Conduct the standard tensile fracture experi-
Figure 1: The experimental equipment.
ment on a set of a specimen to determine the tensile
strength in each case.
Step 2: Choose three commonly used distribution According to the analysis in the previous chapter, the
models to fit the distribution function between the tensile first step of the statistical analysis is to conduct the frac-
stress and the survival rate. Then the tensile stress under ture experiment of the bamboo scrimber. Figure 1 shows
50% survival rate based on the most accurate function is the structural features of the tensile test equipment, from
selected to be the tensile strength. which it can be found that the whole piece was fixed at
Step 3: Conduct the standard short-term tensile creep both ends, and a pair of strain gages were affixed on both
experiment under six different stress levels (from 10 to sides of the specimen. During the experiment process, a
60% of the tensile strength) and record the strain during steady increased tensile force was applied on it until the
the experiment. final fracture.
Step 4: Choose different viscoelastic constitutive models During the whole experimental process, the mes-
to fit the variations of the strain with time to make a com- sages such as the load and displacement were recorded
parative study. In this way, the most accurate model can be using a computer. The experiment was conducted using
determined for further study. the UTM5504-GD microcomputer-controlled test equip-
ment and the serial number of the experiment standard
applied in this case is ASTM D143-09. During the experi-
ment, the temperature is 25°C and the relative humidity is
set to 60%. Using this equipment to conduct the tensile
3 Results test on a set of given specimens, the results are presented
in Table 1:
3.1 The tensile fracture experiment results
In this paper, the bamboo scrimber material was manu- Table 1: The experimental results of the tensile fracture test
factured by a cold-pressing technology. In the first stage
Case Width Thickness Limit Tensile
of this approach, the fibers were immersed in the phenol
number (mm) (mm) tensile strength
resin under high pressure. Then in the second stage, the
load (N) (MPa)
fibers were dried and put into the steel box and com-
pressed to a standard density. The pressure in this stage 1 9.05 5.00 5,239 110.3
2 9.21 5.04 8,314 175.1
is 22 MPa. Finally, in the third stage, the whole mold was
3 9.49 5.15 9,380 197.5
fixed by a set of bolts and placed in an oast house for 12 h. 4 9.33 5.06 6,336 133.4
In this way, the fibers were recombined into a piece to 5 8.97 5.12 6,430 135.4
provide the manufacturing material of the specimen. The 6 9.21 5.05 7,882 165.9
source of the fiber is a kind of phyllostachys pubescens. 7 9.46 5.08 8,751 184.2
8 9.40 5.10 7,749 163.1
The density of this material is 1.08 × 103 kg/m3 and the
9 9.39 5.09 6,949 146.3
moisture content is 5.6%.Applicability of different viscoelasticity constitutive models in bamboo scrimber 365
According to ref. [17], the primary factor of deciding
whether the data can be taken into further analysis is the
coefficient of variation. According to the experiment stan-
dard demands, the value of CV in a set of given data
should not be more than 20% before analysis. In this
paper, the value of this parameter is 17.7%, which can
fulfill the demands of accuracy.
3.2 Statistical analysis of the tensile
strength
In this paper, three kinds of usual distribution functions
in actual engineering applications are applied to make
a comparative study. From the perspective of the best Figure 2: Fitting results of failure rate distribution of the tensile
fitting effect, the constraint function is equivalent to strength.
varying the fitting parameters to obtain the maximum
value of the fitting correlation coefficient. Table 2 and
Figure 2 show the fitting results based on these three 200 N/s and then reduced to 0. Then the static creep load
functions, from which it can be discovered that the fitting was applied to the specimen. For each specimen, the load
errors of the three models are all less than 5%, which is lasts for 6 h.
sufficient for actual engineering application. In addition, As shown in Figure 3, the strain was recorded by an
the estimated values of statistical parameters based on extensometer fixed at the middle part of the specimen
different models are nearly the same, especially for the with the smallest cross-section. The standard of the creep
expected values (the relative difference is less than 2%). experiment applied, in this case, is ASTM D2990-17.
So the tensile strength under the 50% survival rate is During the experiment, the sampling frequency is set to
determined to be 155 MPa. be 1 min.
Table 3 shows the detailed load information of the
creep experiment. Based on the above stress level, six
groups of experiments were conducted. Corresponding
3.3 Tensile creep experiment results experimental results are shown in Figure 4 and Table 4.
The initial strain refers to the strain recorded at the begin-
Based on the strength parameter obtained in the previous ning of the creep experiment, while the final strain refers
section, the creep experiment can be conducted. During to the strain recorded at the end of the experiment. From
the experiment, the temperature and humidity are fixed these six curves, a clear conclusion can be proposed that
to be the same as those in the tensile fracture experiment. the curves of the low-stress level (10 and 20% of the
Before the creep experiment, two load cycles have been tensile strength) are nearly horizontal. The relative incre-
applied on the specimen for a pretreatment, during which ments in both cases are less than 2%, which means that
the load was increased from 0 to 7 kN with the speed of the whole amount of strain was mainly made up of the
Table 2: Fitting functions of failure rate distribution of the tensile strength
Model type Distribution function Estimated value of a statistical parameter Correlation coefficient
Normal μ = 155.7 0.983
y=Φ − ( x − 155.7
29.2 ) σ = 29.2
Lognormal y = Φ (− μ = 152.9 0.966
)
ln x − 5.03
0.2
σ = 29.4
Three-parameter Weibull μ = 156 0.979
y = 1 − exp (1 − ( )
x − 93.9 3.11
72.9 ) σ = 28.6366 Sun Songsong and Wan Maosong
Figure 4: The strain history during the creep experiment.
Figure 3: The creep experiment equipment. 3.4 Creep model analysis
As mentioned above, the creep behavior of the bamboo
elastic strain and the creep behavior under this stress
scrimber changes with the stress level applied to it.
level is not obvious. In addition, the initial strain and
In a previous study, several viscoelasticity constitutive
the final strain are almost correlated linearly with the
models were proposed to research this property of com-
stress. While for the 30, 40, and 50% levels, the creep
posite materials. Among which the Maxwell model is con-
strain increases more obviously with higher slopes.
sidered to be an effective model in analyzing the creep
The relative creep increments within these cases are
behavior [18,19]. This model can exhibit previous rheolo-
much higher than those of the first two cases. This means
gical behavior, which is similar to the creep process. As
that the creep resistance of the material under these
shown in Figure 5, this model is made up of a series
stress levels becomes weaker. For the highest stress level
combination of a spring model and a Newtonian dashpot
(60%), the increasing rate of the strain with the given
model. The stress–strain relationship of this model can
stage becomes unsteady. The unstable accelerated creep
be expressed as follows:
appears although the fracture has not happened so far.
Generally speaking, the creep property of the bamboo σ1 = σ2 = σ0, (1)
scrimber is influenced by the stress level. The values of σ1 = E0 ε1(t ) , (2)
the creep resistance under the low-stress conditions are
dε2 (t )
more obvious than that under the high-stress conditions. σ2 = η0 , (3)
dt
Table 3: Load parameters of the creep experiment Table 4: The initial and final strain state of the creep experiment
Case Width Thickness Stress Stress Case Initial Final Relative
number (mm) (mm) level (%) (MPa) number strain (10−3) strain (10−3) increment (%)
1 9.24 5.03 10 15.5 1 1.01 1.02 1.2
2 9.67 5.01 20 31 2 2.10 2.14 1.8
3 9.34 4.99 30 46.5 3 3.09 3.19 3.2
4 9.09 4.99 40 62 4 4.62 4.82 4.3
5 9.38 5.02 50 77.5 5 5.18 5.41 4.4
6 9.60 5.01 60 93 6 6.5 7.09 9.1Applicability of different viscoelasticity constitutive models in bamboo scrimber 367
Table 5: Model parameters based on the conventional maxwell
model
Case E0 (MPa) η0 (GPa/min) Correlation
number coefficients
Figure 5: The structure features of the Maxwell model.
1 15,346 392,305 0.915
2 14,832 331,197 0.823
3 15,048 129,960 0.697
where σ0 is the static stress generated by the load, t is the
4 13,420 88,787 0.782
time, E0 is the elastic modulus of the material and η0 is 5 14,961 92,781 0.719
the viscosity coefficient. σ1 and σ2 are the stress generated 6 14,308 48,261 0.939
by the spring and the Newtonian dashpot model, respec-
tively. ε1(t ) and ε2 (t ) are the strain response from the
spring and the Newtonian dashpot model, respectively.
According to the previous study, the strain responses of
this model can be expressed as follows:
σ0
ε1(t ) = , (4)
E0
σ0
ε2 (t ) = t, (5)
η0
σ0 σ
ε (t ) = ε1(t ) + ε2 (t ) = + 0 t. (6)
E0 η0
According to the definition of the traditional Maxwell
model, both the parameters E0 and η0 can be treated
as material constants. Based on the experiment results
above, the parameters of the model can be determined
by a fitting approach. The theoretical basis of the process
can be expressed as follows:
(1) The initial values of the strain obtained based on
the experiment data and the response equation are Figure 6: Fitting results based on the conventional Maxwell model
and 10% stress level.
the same.
σ
ε (t = 0) = 0 . (7)
E0
(2) The sum of the relative difference percentage between
the experiment data and the response equation is the
minimum. The definition of the relative difference
percentage is:
n
ε (ti ) − εei
f= ∑ , (8)
i=1
εei
where f is the relative difference percentage and ε (ti )
and εei are the values of the strain obtained by the
response equation and the experiment at the ith time
node. Based on this assumption, the model para-
meters in each set can be determined. The results
are shown in Table 5 and Figures 6–11.
As shown in Figures 6–11, a clear conclusion can be
proposed that the values of the strain obtained by the
experiment and the response function are quite different Figure 7: Fitting results based on the conventional Maxwell model
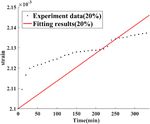
from each other. In addition, the parameters in each set and 20% stress level.368 Sun Songsong and Wan Maosong
Figure 10: Fitting results based on the conventional Maxwell model
Figure 8: Fitting results based on the conventional Maxwell model and 50% stress level.
and 30% stress level.
Figure 9: Fitting results based on the conventional Maxwell model Figure 11: Fitting results based on the conventional Maxwell model
and 40% stress level. and 60% stress level.
are obviously different from those in other set, which can According to previous research, the fractional-order
be attributed to the diversity of the material. Besides, model usually has the time-variant characteristic. In
some of the correlation coefficients of the fitting results a previous study, some experts applied this theory to
are mainly less than 90%, which means that the relative research the creep behavior of some geologic materials
error in these sets are more than 10%. This accuracy can such as rock and clay [20,21]. The application of this
not fulfill the actual engineering demands. The main approach in bamboo material has rarely been reported.
reason for this phenomenon may be the definition of In addition, the creep behavior research based on the
the viscosity coefficient η0 . In the traditional application fractional-order theory is usually long-term type, the
of the Maxwell model, this parameter is usually consid- applicability of this theory in short-term creep behavior
ered to be a material constant. While in recent years, is still unclear. In this paper, we applied this theory to fit
some experts discovered that this parameter has a time- the short-term creep strain curve to make a comprehen-
variant characteristic. sive comparative study.Applicability of different viscoelasticity constitutive models in bamboo scrimber 369
Up to now, there are several fractional models such
as the Riemann–Liouville (RL) model, the Caputo model,
and so on. According to the previous study, the RL model
seems to be appropriate for viscoelastic materials [22]. So
in this paper, we applied this model in bamboo scrimber
short-term creep behavior research. The definition of this
model can be expressed as refs. [23–26]:
t
dα 1 d
dt α
[ f (t )] =
Γ(1 − α ) d t
∫ (t f−(ττ))α dτ (9)
0
where Γ represents the gamma function and α(0 < α < 1))
is the order. According to this model, the strain response
during the creep stage can be determined. The stress–
strain relationship of the Maxwell model can be expressed
as follows:
Figure 13: Fitting results based on the fractional defined Maxwell
σ0
ε1(t) = , (10) model and 20% stress level.
E0
σ0 tα
ε2 (t) = , (11)
η0 Γ(α + 1)
σ0 σ tα
ε (t ) = ε1(t ) + ε2 (t ) = + 0 . (12)
E0 η0 Γ (α + 1)
Compared with the conventional Maxwell model, this
modified model has one more parameter in all. Based on
this response function and the experimental results, the
parameters of the model can be determined. Figures
12–17 and Table 6 show the fitting results based on this
modified Maxwell model, a clear comparison can be
found that compared with the traditional model, this
fractional order-defined model can exhibit much higher
Figure 14: Fitting results based on the fractional defined Maxwell
model and 30% stress level.
accuracy in expressing the creep strain curve. The values
of the strain obtained based on the response function
are quite near to those from the experiment data at
the same time nodes. Among the six groups, the correla-
tion coefficients are all over 98.5%, which makes it com-
pletely enough for engineering applications. Besides, the
values of the parameter α in every set based on the fitting
results are located within its definition range (from 0 to 1).
Thus, this model is more suitable for actual engineering
applications.
Figure 12: Fitting results based on the fractional defined Maxwell In a previous study, some experts found that the
model and 10% stress level. Burgers viscoelasticity constitutive model which has370 Sun Songsong and Wan Maosong
Figure 15: Fitting results based on the fractional defined Maxwell Figure 17: Fitting results based on the fractional defined Maxwell
model and 40% stress level. model and 60% stress level.
Table 6: Model parameters based on the fractional defined Maxwell
model
Case number α Correlation coefficients
1 0.324 0.985
2 0.607 0.987
3 0.431 0.998
4 0.474 0.997
5 0.378 0.998
6 0.646 0.999
conducted to obtain the tensile strength of the material.
Then, six sets of short-term tensile creep experiments
were done to obtain the strain history throughout the
Figure 16: Fitting results based on the fractional defined Maxwell whole process. Finally, different models were applied in
model and 50% stress level. analyzing the creep property of the material. Corresponding
conclusions are shown as follows:
four parameters according to its definition could get a (1) The tensile strength experiment results show obvious
high accuracy in fitting the tensile creep strain curve. randomness property. Based on the commonly used
Compared with this model, the modified Maxwell model distribution models, the tensile strength under the
proposed in this paper can fit the strain curve well with 50% survival rate can be determined. The results
fewer parameters. This makes it superior to the other from different models are nearly the same.
models in engineering applications. (2) Compared with the traditional model, the combined
fractional and Maxwell model can provide much
higher accuracy in fitting the creep strain curve,
thus it is more suitable for engineering applications.
4 Discussion and conclusion
This study mainly focuses on researching the effects
The short-term tensile creep behavior of the bamboo of stress levels on the tensile creep properties of bamboo
scrimber is selected as the object of this study. First, sev- scirmber and the short-term strain predictive model under
eral sets of standard tensile fracture experiments were certain conditions of temperature and humidity. However,Applicability of different viscoelasticity constitutive models in bamboo scrimber 371
many factors, such as temperature and humidity, affect the [11] Li H, Zhang H, Qiu Z. Mechanical properties and stress strain
creep of bamboo scrimber. Additionally, the parameters relationship models for bamboo scrimber. J Renew Mater.
based on different fitting results show an obvious random 2020;8(1):13–27.
[12] Yang W, Xuewei JI, Maojun D. Model for axial stress–strain
property. So more properties of the creep behavior of the
relationship of bamboo scrimber. Acta Materiae Compositae
bamboo scirmber will be the focus of the next phase of Sin. 2018;35(3):572–9.
research. [13] Li H-T, Zhang Q-S, Wu G. Stress–strain model under com-
pression for side pressure laminated bamboo. J Southeast
Conflict of interest: Authors state no conflict of interest. Univ (Nat Sci). 2015;45(6):1130–4.
[14] Zhang Y, Wang A. remaining useful life prediction of rolling
bearings using electrostatic monitoring based on two-stage
information fusion stochastic filtering. Math Probl Eng.
March 17, 2020;2020:2153235.
References [15] Wang A, Zhang Y, Zuo H. Assessing the performance degra-
dation of lithium-ion batteries using an approach based on
[1] Hong C, Li H, Xiong Z, Lorenzo R, Corbi I, Corbi O, et al. Review fusion of multiple feature parameters. Math Probl Eng.
on connections for Engineered bamboo structures. J Build Eng. 2019;2019:3091071.
2020;30:101324. [16] Chang CC, Zheng YP, Sun WM, Ma Z. LPV estimation of SOC
[2] Li X, Ashraf M, Li H, Zheng X, Al-Deen S, Wang H, et al. based on electricity conversion and hysteresis characteristic.
Experimental study on the deformation and failure mechanism J Energy Eng. 2019;145(6):04019026.
of Parallel Bamboo Strand Lumber under drop-weight pene- [17] Wei Y, Zhou M, Yuan L. Mechanical performance of glulam
tration impact. Constr Build Mater. 2020;242:118135. bamboo columns under eccentric loading. Acta Mater Comp
[3] Tan C, Li H, Wei D, Lorenzo R, Yuan C. Mechanical performance Sin. 2016;33(2):379–85.
of parallel bamboo strand lumber columns under axial com- [18] Stan F, Turcanu A-M, Fetecau C. Analysis of viscoelastic
pression: experimental and numerical investigation. Constr behavior of polypropylene/carbon nanotube nanocomposites
Build Mater. 2020;231:117168. by instrumented indentation. Polymers. 2020;12:2535.
[4] Li H, Zhang H, Qiu Z, Su J, Wei D, Lorenzo R, et al. Mechanical [19] Peng G. Nanoindentation creep of nonlinear viscoelastic
properties and stress strain relationship models for bamboo polypropylene. Polym Test. 2015;43:38–43.
scrimber. J Renew Mater. 2020;8(1):13–27. [20] Peng R, Peng W, Hua Z. Nonlinear behavior of clay creep and
[5] He W, Song J, Wang T, Li J, Xie L, Yang Y, et al. Effect of heat oil its fractional derivative creep model. Eng Mech.
treatment on bamboo scrimber properties. J Forestry Eng. 2020;32(9):153–60.
2017;2(5):15–9. [21] Zhilei H, Dezhen Z, Mingli Z, Zhi-jing L. An unsteady creep
[6] Naresworo N, Naoto A. Development of structural composite constitutive model based on fractional order derivatives. Rock
products made from bamboo I: fundamental properties of Soil Mech. 2016;37(3):737–44.
bamboo zephyr board. J Wood Sci. 2000;46(1):68–74. [22] Xu J, Chen Y, Tai Y. Vibration analysis of complex fractional
[7] Naresworo N, Naoto A. Development of structural composite viscoelastic beam structures by the wave method. Int J Mech
products made from bamboo II: fundamental properties of Sci. 2020;167:105204.
laminated bamboo lumber. J Wood Sci. 2001;47(3):237–42. [23] Tian J, Ding J, Zhang C, Luo S. Four-wheel differential
[8] Huang D, Sheng B, Shen Y. An analytical solution for double steering control of IWM driven evs. IEEE Access.
cantilever beam based on elastic-plastic bilinear cohesive law: 2020;8:152963–73.
Analysis for mode I fracture of fibrous composites. Eng Fract [24] Xu X, Jiang Y, Chen N, Lee HP. Dynamic behavior of a vehicle
Mech. 2018;02(193):66–76. with rear axle compliance steering. J Vibroeng.
[9] Huang D, Bian Y, Huang D. An ultimate-state-based-model for 2017;19(6):4483–97.
inelastic analysis of intermediate slenderness PSB columns [25] Tai Y, Chen N, Wang L, Feng Z, Xu J. A numerical method for
under eccentrically compressive load. Constr Build Mater. a system of fractional differential – algebraic equations
2015;06(94):306–14. based on sliding mode control. Mathematics.
[10] Huang D, Bian Y, Zhou A. Experimental study on stress–strain 2020;8:1134.
relationships and failure mechanisms of parallelstrand [26] Chang C, Zheng Y, Yu Y. Estimation for battery state of charge
bamboo made from Phyllostachys. Constr Build Mater. based on temperature effect and fractional extended Kalman
2015;01(77):130–8. filter. Energies. 2020;13:5947.You can also read