Robust Pandemic Control Synthesis with Formal Specifications: A Case Study on COVID-19 Pandemic
←
→
Page content transcription
If your browser does not render page correctly, please read the page content below
Robust Pandemic Control Synthesis with Formal Specifications: A Case
Study on COVID-19 Pandemic
Zhe Xu, Xiaoming Duan
Abstract— Pandemics can bring a range of devastating conse- [1], robotics [2], power systems [3], etc. On the agent-
quences to public health and the world economy. Identifying the level, temporal logic formulas can express specifications
most effective control strategies has been the imperative task for people in both indoor and outdoor spaces to obey the
all around the world. Various public health control strategies
pandemic requirements (e.g., social distancing requirements).
arXiv:2103.14262v1 [eess.SY] 26 Mar 2021
have been proposed and tested against pandemic diseases (e.g.,
COVID-19). We study two specific pandemic control models: the For example, according to the United States Centers for
susceptible, exposed, infectious, recovered (SEIR) model with Disease Control and Prevention (CDC) guidelines, a close
vaccination control; and the SEIR model with shield immunity contact is defined as “any individual who was within 6
control. We express the pandemic control requirement in metric feet of an infected person for at least 15 minutes starting
temporal logic (MTL) formulas. We then develop an iterative ap-
proach for synthesizing the optimal control strategies with MTL from 2 days before illness onset until the time the patient is
specifications. We provide simulation results in two different isolated”. This can be expressed by a temporal logic formula
scenarios for robust control of the COVID-19 pandemic: one for ♦[t1 −2d,t2 ] [0,15min] (kpcontact − pinf ected k ≤ 6f eet), where
vaccination control, and another for shield immunity control, t1 and t2 denote the time of illness onset of the infected
with the model parameters estimated from data in Lombardy, person and the time the patient is isolated, respectively;
Italy. The results show that the proposed synthesis approach
can generate control inputs such that the time-varying numbers pinf ected and pcontact denote the positions of the infected
of individuals in each category (e.g., infectious, immune) satisfy person and the individual to be identified as a close contact,
the MTL specifications with robustness against initial state and respectively.
parameter uncertainties. In [4], we provided the first systematic control synthesis
approach for three control strategies against COVID-19 with
I. I NTRODUCTION MTL specifications expressing the requirements for the con-
Pandemics can bring a range of devastating consequences trol outcomes. In this paper, we extend [4] in the following
to public health and the world economy. Identifying the most main aspects. (1) We investigate the robust pandemic control
effective control strategies has been the imperative task all synthesis problem that takes into account initial state and
around the world. Various public health control strategies parameter uncertainties (which were not considered in [4]).
have been proposed and tested against pandemic diseases (2) For the pandemic control models that we consider, we
(e.g., COVID-19). However, the existing pandemic control derive the theoretical bounds for the robustness degree of
synthesis approaches still suffer from several limitations: (a) any trajectory within the initial state and parameter un-
The current control synthesis approaches do not take into certainty ranges with respect to an MTL specification. (3)
account the uncertainties in the states and parameters. (b) Based on the derived theoretical bounds, we develop an
There is a lack of specific and formal specifications for the iterative optimization-based approach and in each iteration
expected effects and outcomes of the control strategies. we solve a mixed-integer bi-linear programming problem (for
A specification for a biological system describes its vaccination control) or mixed-integer fractional constrained
desirable behaviors and formalizes its properties. On the programming problem (for shield immunity control [5]).
population-level, specifications such as “the infected people We provide simulation results in two different scenarios
should never exceed one thousand per day within the next for robust control of the COVID-19 pandemic: one for vacci-
90 days, and the immune people should eventually exceed nation control, and another for shield immunity control, with
6 million after 40 to 60 days”, which can be expressed the model parameters estimated from data in Lombardy, Italy.
as a temporal logic formula [0, 90d] (Inf ectedP erDay ≤ The results show that the proposed synthesis approach can
1000) ∧ ♦[40d, 60d] (Immune ≥ 6, 000, 000), can be used for generate control inputs such that the time-varying numbers
the formal synthesis of pandemic control strategies such as of individuals in each category (e.g., infectious, immune)
vaccination, quarantine, and shield immunity. Such temporal satisfy the MTL specifications with robustness against initial
logic formulas have been used as high-level knowledge or state and parameter uncertainties.
specifications in many applications in artificial intelligence II. R ELATED W ORK
Zhe Xu is with the School for Engineering of Matter, Trans- Modeling and optimal control of pandemics: There have
port, and Energy, Arizona State University, Tempe, AZ 85287. email: been numerous research focusing on modeling the infection
{xzhe1@asu.edu}. of pandemic diseases. Among the various models, com-
Xiaoming Duan is with the Oden Institute for Computational Engineering
and Sciences, University of Texas, Austin, Austin, TX 78712. Email: partmental models such as the susceptible, infectious, and
{xiaomingduan.zju@gmail.com}. recovered (SIR) model [6] and its variations [7], [8], [9], [10],[11], [12] have been commonly used. More detailed models (k ∈ I). Then the Boolean semantics of MTL are defined
have also been proposed to incorporate the hospitalized pop- recursively as follows [36]:
ulation [13] and differentiate symptomatic and asymptomatic
hh>ii(ξ, k) :=>,
infected populations [12], [14], [15]. There exist work in
optimal control based on compartmental models [16], [17]. hhπii(ξ, k) := ξk ∈ O(π) ,
On the other hand, agent-based models have been increas- hh¬φii(ξ, k) :=¬hhφii(ξ, k),
ingly used by researchers to examine complex urban health hhφ1 ∨ φ2 ii(ξ, k) :=hhφ1 ii(ξ, k) ∨ hhφ2 ii(ξ, k),
problems and has been recently applied to study pandemics _ ^
[18], [19], [20], [21], [22]. While these models consider the hhφ1 UI φ2 ii(ξ, k) := hhφ2 ii(ξ, k 0 ) ∧ hhφ1 ii
k0 ∈(k+I) k≤k00 , k) := + ∞,
III. M ETRIC T EMPORAL L OGIC , T RAJECTORIES , AND
I NTERVAL T RAJECTORIES ρ(ξ, π, k) :=Distd (ξk , O(π)),
In this section, we briefly review metric temporal logic ρ(ξ, ¬φ, k) := − ρ(ξ, φ, k),
(MTL) [35]. The state x (e.g., representing the susceptible, ρ(ξ, φ1 ∨ φ2 , k) := max ρ(ξ, φ1 , k), ρ(ξ, φ2 , k) , (2)
exposed, infectious, recovered population of a certain region)
ρ(ξ, φ1 UI φ2 , k) := 0 max min ρ(ξ, φ2 , k 0 ),
belongs to the domain X ⊂ Rn≥0 . The time set is T = R≥0 . k ∈(k+I)
The domain B = {True, False} is the Boolean domain, and 00
min ρ(ξ, φ1 , k ) .
the time index set is I = {0, 1, . . . }. We use ξ : T 7→ X 00 0
k≤k | π | ¬φ | φ1 ∧ φ2 | φ1 ∨ φ2 | φ1 UI φ2 , by [ξ, ξ], as a set of trajectories such that for any trajectory
ξ ∈ [ξ, ξ] we have ξk ∈ [ξ k , ξ k ] holds for all k. For an
where > stands for the Boolean constant True, π ∈ AP
interval trajectory [ξ, ξ], we define its nominal trajectory ξ ∗
is an atomic proposition, ¬ (negation), ∧ (conjunction), ξ +ξ k
∨ (disjunction) are standard Boolean connectives, U is a such that ξk∗ = k
2 for all k.
temporal operator representing “until”, I is a time index
interval of the form I = [i1 , i2 ] (i1 ≤ i2 , i1 , i2 ∈ I). In We use ρ([ξ, ξ], φ, k) to denote the robustness degree of
the remaining of this paper, we will use day as the unit an interval trajectory [ξ, ξ] with respect to the formula φ at
in I. We can also derive two useful temporal operators time instant t[k] (k ∈ I), and ρ([ξ, ξ], φ, k) is defined as
from “until” (U), which are “eventually” ♦I φ = >UI φ and
“always” I φ = ¬♦I ¬φ. ρ([ξ, ξ], φ, k) := min ρ(ξ, φ, k). (3)
ξ∈[ξ,ξ]
We define the set of states that satisfy the atomic proposi-
tion π as O(π) ⊂ X . We denote hhφii(ξ, k) = > if the state Intuitively, if ρ([ξ, ξ], φ, k) ≥ 0, then any trajectory ξ ∈ [ξ, ξ]
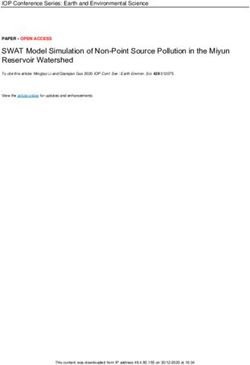
of the trajectory ξ satisfies the formula φ at time instant t[k] satisfied the MTL formula φ at time instant t[k].IV. PANDEMIC SEIR M ODEL WITH C ONTROL (a) vaccination V
control
S TRATEGIES
In this section, we study the susceptible, exposed, infec- (b)
vaccination
shield
immunity
tious, recovered (SEIR) model for pandemics [8], [5], [11] control
with vaccination control and shield immunity control, and
provide the problem formulation for robust pandemic control
S E I R
with formal specifications. birth
susceptible exposed infectious immune
As shown in Figure 1, the total population is divided into
five parts in an SEIR model:
• The susceptible population S: everyone is susceptible to natural death
D
the disease by birth since immunity is not hereditary; dead from
infection
• The exposed population E: the individuals who have
been exposed to the disease, but are still not infectious; Fig. 1. Block diagram of the pandemic SEIR model with (a) vaccination
• The infectious population I: the individuals who are control and (b) shield immunity control.
infectious;
• The immune (recovered) population R: the individuals
who are vaccinated or recovered from the disease, i.e., where the states and parameters are the same as in (4), while
the population who are immune to the disease; χ is the shield strength [5] as control input to be synthesized
• The dead population D: the deaths from the disease. for the recovered population to substitute the contact for the
Vaccination control model: We consider the SEIR model susceptible population.
[8], [37] with vaccination control as follows. We rewrite (4) and (5) in the following general form.
I˙ = E − (γ + µ + α)I; ẋ = f (x, u, θ), (6)
T
Ė = βSI/N − (µ + )E; where the state x = [I, E, S, R, D] ∈ the control in- R5≥0 ,
Ṡ = λN − µS − βSI/N − V ; (4) put u represents V for the vaccination control and represents
χ for the shield immunity control, θ = [α, β, , γ, µ, λ], and
Ṙ = γI − µR + V ; f : R5≥0 × R≥0 × R6≥0 → R5≥0 is a smooth vector field
Ḋ = −I˙ − Ė − Ṡ − Ṙ, according to (4) and (5).
For computational efficiency, we discretize the dynamics
where the control input V is the number of vaccinated
in (6) as follows.
individuals per day, N = S + E + I + R ≤ N0 is
the total population in the region (N0 is the initial total x(k + 1) = f¯(x[k], u[k], θ), (7)
population in the region), S, E, I, and R are the number
of susceptible, exposed, infectious and recovered population where f¯(·, ·, ·) is discretized from f (·, ·, ·) in (6) using
in the region, respectively, and D is the number of deaths Euler’s method.
from the pandemic disease in the region. For the parameters, Now we provide the problem formulation of the robust
λ denotes the per-capita birth rate, µ is the per-capita natural pandemic control synthesis problem as follows.
death rate (death rate from causes unrelated to the pandemic Problem 1 (Robust pandemic control): Given the SEIR
disease), α is the pandemic virus-induced average fatality control model in (7) and an MTL specification φ, compute
rate, β is the probability of disease transmission per contact the control input signal u[·] that minimizes the control effort
(dimensionless) times the number of contacts per unit time, ku[·]k (here k·k denotes the `2 norm), while guaranteeing
is the rate of progression from exposed to infectious (the ρ([ξ, ξ], φ, 0) ≥ 0, where [ξ, ξ] is the interval trajectory
reciprocal is the incubation period), and γ is the recovery starting with x[0] ∈ [x[0], x[0]] with the control input signal
rate of infectious individuals. We assume that the birth rate u[·] and parameter θ ∈ [θ, θ].
and the natural death rate are the same for the population V. S OLUTION
we are investigating, i.e., λ = µ, and as a result, D = The robust pandemic control synthesis problem can be
N0 − I − E − S − R = N0 − N holds. formulated as a robust optimization problem as follows.
Shield immunity control model: We consider the SEIR
model with shield immunity control [5] as follows (see Fig. min ku[·]k
u[·]
1 (b) as an illustration).
s.t. x[k + 1] = f¯(x[k], u[k], θ), ∀k = 0, . . . , T,
I˙ = E − (γ + µ + α)I; ∀x[0] ∈ [x[0], x[0]], ∀θ ∈ [θ, θ], (8)
Ė = βSI/(N + χR) − (µ + )E; 0 ≤ u[k] ≤ umax , ∀k = 0, . . . , T,
Ṡ = λN − µS − βSI/(N + χR); (5) ρ([ξ, ξ], φ, 0) ≥ 0,
Ṙ = γI − µR;
where [ξ, ξ] is the interval trajectory starting with x[0] ∈
Ḋ = −I˙ − Ė − Ṡ − Ṙ, [x[0], x[0]] with the control input signal u[·] and parameterθ ∈ [θ, θ], and T ∈ I is the maximal time index we consider. specification φ with robustness of at least δmax .
Generally, the optimization problem in (8) is a robust min ku[·]k
mixed-integer non-linear programming problem. We refer the u[·]
readers to [29] for a detailed description of how the constraint s.t. x∗ [k + 1] = f¯(x∗ [k], u[k], θ∗ ), ∀k = 0, . . . , T, (9)
ρ(ξ, φ, 0) ≥ 0 is encoded to satisfy an MTL specification φ. 0 ≤ u[k] ≤ umax , ∀k = 0, . . . , T,
The integer variables are introduced when a big-M formula-
ρ(ξ ∗ , φ, 0) ≥ δmax .
tion [38] is needed to satisfy MTL specifications that contain
♦I or ∨. In (9), we approximate the total population N with the
To efficiently solve the robust optimization problem in (8), initial population N0 as the change of N is relatively small
we first provide the following theorem. compared to the multiplication of the susceptible population
and the infectious population. With such an approximation,
Theorem 1: Given an interval trajectory [ξ, ξ] and its the optimization problem becomes a mixed-integer bi-linear
nominal trajectory ξ ∗ , then for any ξ ∈ [ξ, ξ] and any programming problem (for vaccination control) or mixed-
k ∈ {0, 1, . . . , K}, we have integer fractional constrained programming problem (for
ρ(ξ ∗ , φ, k) − δmax ≤ ρ(ξ, φ, k) ≤ ρ(ξ ∗ , φ, k) + δmax , shield immunity control), which can be efficiently solved
through solvers such as GEKKO [39].
where φ is any MTL formula, δmax , max δk , and δk = If the constrained optimization problem in (9) is infeasible
k
ξi −ξi i (e.g., due to the conservativeness of the bound δmax ), we will
max k 2 k , and ξ k is the i-th dimension value of ξ k . re-solve (9) by replacing δmax with ζ − ρ([ξ, ξ], φ, 0) (where
i
From Theorem 1, it can be seen that if we can design the ζ is initially set as 0). After we obtain the optimal control
control input signal such as ρ(ξ ∗ , φ, k) ≥ δmax , then we have input signal u∗ [·] from solving (9), we compute interval
ρ(ξ, φ, k) ≥ 0 holds for any ξ ∈ [ξ, ξ], i.e., ρ([ξ, ξ], φ, k) ≥ 0. trajectory [ξ, ξ] with u∗ for x[0] ∈ [x[0], x[0]], θ ∈ [θ, θ].
ξi −ξi Then we compute ρ([ξ, ξ], φ, 0) based on (2) and (3). If
However, as δk = max k 2 k depends on u, δmax also
i ρ([ξ, ξ], φ, 0) ≥ 0, then the algorithm terminates with the
depends on u. Therefore, we need to design an iterative
solution u∗ ; otherwise, we update ζ as ζ − ρ([ξ, ξ], φ, 0) and
approach to compute u such that ρ(ξ ∗ , φ, k) ≥ δmax . Such
repeat the above procedures until either ρ([ξ, ξ], φ, 0) ≥ 0
an iterative approach is shown in Algorithm 1.
holds or a maximal number of iterations (denoted as Itermax )
is reached.
Algorithm 1 Robust pandemic control synthesis with MTL
specifications. VI. S IMULATION R ESULTS
1: Inputs: [x[0], x[0]], [θ, θ], f¯ In this section, we implement the proposed robust control
2: Initialize ζ ← 0, u synthesis methods in the COVID-19 models estimated from
3: Compute interval trajectory [ξ, ξ] with control input data in Lombardy, Italy.
signal u[·] for x[0] ∈ [x[0], x[0]], θ ∈ [θ, θ]
A. Robust Vaccination Control for COVID-19
4: Compute ρ([ξ, ξ], φ, 0) and δmax
5: Iter ← 1 The parameters of the COVID-19 SEIR model with un-
6: while (ρ([ξ, ξ], φ, 0) < 0) ∧ (Iter < Itermax ) do certainties are shown in Table I. They were estimated in
7: Solve (9) to obtain the optimal control input signal [8] from the data in the early days (from February 23
u∗ [·] with robustness δmax to March 16, 2020) in Lombardy, Italy with no isolation
8: if (9) is infeasible then measures. The start time for the simulations in this subsection
9: ζ ← ζ − ρ([ξ, ξ], φ, 0) is February 23, 2020. We consider three MTL specifications
10: Solve (9) to obtain the optimal control inputs u∗ as shown in Table II. For example, φ1V = [0,100] (I ≤
with robustness ζ (i.e., replace δmax with ζ in (9)) 0.3) ∧ [0,100] (D ≤ 0.05) ∧ ♦[40,60] (R ≥ 8), which means
11: end if “the infected population should never exceed 0.3 million and
12: u[·] ← u∗ [·] the deceased population should never exceed 0.05 million
13: Compute interval trajectory [ξ, ξ] with u for x[0] ∈ within the next 100 days, and the immune population should
[x[0], x[0]], θ ∈ [θ, θ] eventually exceed 8 million after 40 to 60 days”. We choose
14: Compute ρ([ξ, ξ], φ, 0) and δmax the initial values of the states with uncertainties as I[0] =
15: Iter ← Iter + 1 1000 ± 1000 (people), E[0] = 0.02 ± 0.001 million, S[0] =
16: end while 9.979 ± 0.001 million, R[0] = 0 and D[0] = 0.
17: Return u We used the the CORA toolbox [40] to compute [ξ, ξ] with
the initial state and parameter uncertainties. We use the solver
GEKKO [39] to solve the optimization problems formulated
In each iteration in the while loop, we solve the following in Section V. We set Itermax = 100, while in reality the
optimization problem for synthesizing the control input sig- algorithm terminates in all cases within three iterations with
nal u[·] such that the nominal trajectory satisfies the MTL feasible and optimal solutions. Fig. 2 and Table II showTABLE I
B. Robust Shield Immunity Control for COVID-19
PARAMETERS OF COVID-19 SEIR MODEL ESTIMATED FROM DATA
FROM L OMBARDY, I TALY FROM F EBRUARY 23 TO M ARCH 16 (2020) We use the same initial state and parameter values of
WITH NO ISOLATION MEASURES [8] WITH UNCERTAINTIES . the COVID-19 SEIR model with uncertainties as shown in
Table I. The start time for the simulations in this subsection
parameter value parameter value is February 23, 2020. We set the three MTL specifications
0.2±0.001/day λ 1/30295 ϕ1S , ϕ2S and ϕ3S (as shown in Table III) to be less stringent
γ 0.2±0.001/day µ 1/30295 than the MTL specifications with the vaccination control, as
α 0.006±0.001/day N0 10 million shield immunity is generally less effective than vaccination.
β 0.75±0.001/day Ts 1 day We investigate the hypothetical scenario where the isolation
measures are replaced by shield immunity control.
Fig. 3 and Table III show the simulation results for shield
TABLE II immunity control of the COVID-19 SEIR model with MTL
MTL SPECIFICATIONS AND SIMULATION RESULTS FOR VACCINATION specifications ϕ1S , ϕ2S and ϕ3S , respectively. The results show
CONTROL . that, despite the initial state and parameter uncertainties, the
MTL specifications ϕ1S , ϕ2S and ϕ3S are satisfied respectively.
control computation time We observe that with the three MTL specifications, the syn-
MTL specification thesized shield immunity control input signals all increase to
effort (each iteration)
φ1V = [0,100] (I ≤ 0.3) a peak after approximately 20 to 40 days and then gradually
∧ [0,100] (D ≤ 0.05) 1.28 1.365 s decrease. These observations indicate that shield immunity
∧ ♦[40,60] (R ≥ 8) at early days of COVID-19 is more efficient than shield
φ2V = [0,100] (I ≤ 0.15) immunity at later days. The results also show that more
∧ [0,100] (D ≤ 0.02) 2.397 1.134 s control efforts are needed for more stringent specifications.
∧ ♦[40,60] (R ≥ 9)
φ3V = [0,100] (I ≤ 0.1) VII. C ONCLUSION
∧ [0,100] (D ≤ 0.01) 6.934 3.289 s
∧♦[40,60] (R ≥ 9) In this paper, we proposed a systematic control synthesis
approach for mitigating a pandemic based on two control
models with vaccination and shield immunity, respectively.
TABLE III The proposed approach can synthesize control inputs that
MTL SPECIFICATIONS AND SIMULATION RESULTS FOR SHIELD lead to satisfaction of metric temporal logic specifications
IMMUNITY CONTROL . despite the state and parameter uncertainties.
We list two future directions as follows. First, we will
control computation time extend this work to online control synthesis so that the states
MTL specification and parameters can be updated periodically with the latest
effort (each iteration)
1
ϕS = [0,100] (I ≤ 0.6) disease infection data. Second, we will study the benefits and
∧ [0,100] (D ≤ 0.1) 33349.80 3.498 s costs of joint control of different control strategies so that the
∧ ♦[40,60] (R ≥ 1) specifications can be satisfied with coordinated efforts.
2
ϕS = [0,100] (I ≤ 0.5)
∧ [0,100] (D ≤ 0.07) 84272.22 3.312 s A PPENDIX
∧ ♦[40,60] (R ≥ 1)
ϕ3S = [0,100] (I ≤ 0.3) Proof of Theorem 1:
∧ [0,100] (D ≤ 0.06) 122476.59 2.385 s To prove Theorem 1, we first prove that Theorem 1 holds
∧♦[40,60] (R ≥ 1) for any atomic proposition π.
As the metric d satisfies the triangle inequality, for any k,
we have that for any ξk ∈ [ξ k , ξ k ] and any y ∈ X ,
d(ξk∗ , y) − d(ξk∗ , ξk ) ≤ d(ξk , y) ≤ d(ξk∗ , y) + d(ξk∗ , ξk ).
the simulation results for vaccination control of COVID- (10)
19 SEIR model with MTL specifications φ1V , φ2V and φ3V ,
ξi −ξi
respectively. The results show that, despite the initial state As d(ξk∗ , ξk ) ≤ max k 2 k = δk , we have
and parameter uncertainties, the MTL specifications φ1V , φ2V i
and φ3V are satisfied with the synthesized vaccination control d(ξk∗ , y) − δk ≤ d(ξk , y) ≤ d(ξk∗ , y) + δk . (11)
input signals respectively. It can be seen that vaccination
within the first 40 days after the outbreak can mitigate the 1) ξk∗ ∈ O(π), and [ξ k , ξ k ] ⊂ O(π), as shown in Fig. 4
spread of COVID-19 in the most efficient manner. The results (a). In this case, for any ξk ∈ [ξ k , ξ k ],
also show that more control efforts are needed for more
stringent specifications. ρ(ξ, π, k) = inf{d(ξk , y)|y ∈ X \O(π)}.0.5
0.4
vaccinated (M) per day
0.3
0.2
0.1
0
-0.1
-0.2
0 20 40 60 80 100
t (day)
0.5
0.4
vaccinated (M) per day
0.3
0.2
0.1
0
-0.1
-0.2
0 20 40 60 80 100
t (day)
0.6 0.4 0.06
infected population (M)
deceased population (M)
0.05
vaccinated (M) per day
0.4 0.3
0.04
0.2 0.2 0.03
0.02
0 0.1
0.01
-0.2 0 0
0 20 40 60 80 100 0 20 40 60 80 100 0 20 40 60 80 100
t (day) t (day) t (day)
Fig. 2. Optimal vaccination control input signals and interval trajectories (plotted with shading) for COVID-19 SEIR model with robust vaccination
control and MTL specifications ϕ1V (first row), ϕ2V (second row) and ϕ3V (third row). The red and blue lines indicate the thresholds that should never be
exceeded and should eventually be exceeded in the atomic propositions of the MTL specifications, respectively.
40
30
shield strength
20
10
0
0 20 40 60 80 100
t (day)
60
50
40
shield strength
30
20
10
0
0 20 40 60 80 100
t (day)
70
60
50
shield strength
40
30
20
10
0
0 20 40 60 80 100
t (day)
Fig. 3. Optimal shield immunity control input signals and interval trajectories (plotted with shading) for COVID-19 SEIR model with robust shield
immunity control and MTL specifications ϕ1S (first row), ϕ2S (second row) and ϕ3S (third row). The red and blue lines indicate the thresholds that should
never be exceeded and should eventually be exceeded in the atomic propositions of the MTL specifications, respectively.⇠k⇤ 4 (d). In this case,
[⇠ k , ⇠ k ] ⇠k⇤ ρ(ξ ∗ , π, k) = −inf{d(ξk∗ , y)|y ∈ cl(O(π))}.
For any ξk ∈ [ξ k , ξ k ] and ξk ∈
/ O(π),
⇠k⇤
⇠k⇤ ρ(ξ, π, k) = −inf{d(ξk , y)|y ∈ cl(O(π))}
⇠k
≥ −inf{d(ξk∗ , y) + δk |y ∈ cl(O(π))}
= ρ(ξ ∗ , π, k) − δk .
Therefore, ρ(ξ, π, k) ≥ min{X1 , X2 } = X1 ≥ ρ(ξ ∗ , π, k) −
Fig. 4. Four different cases in the proof: (a) ξk∗ ∈ O(π), [ξ k , ξ k ] ⊂ O(π); δk .
(b) ξk∗ ∈
/ O(π), [ξ k , ξ k ] ⊂ X \O(π); (c) ξk∗ ∈ O(π), [ξ k , ξ k ] 6⊂ O(π);
In sum, we have proven that ρ(ξ, π, k) ≥ ρ(ξ ∗ , π, k) − δk .
(d) ξk∗ ∈
/ O(π), [ξ k , ξ k ] 6⊂ X \O(π).
Similarly, we can prove that ρ(ξ, π, k) ≤ ρ(ξ ∗ , π, k) + δk .
Therefore, Theorem 1 holds for any atomic proposition π.
Next, we use induction to prove that Theorem 1 holds for
Thus from (11), we have any MTL formula φ.
ρ(ξ, π, k) ≥ inf{d(ξk∗ , y) − δk |y ∈ X \O(π)} (ii) We assume that Theorem 1 holds for φ and prove
Theorem 1 holds for ¬φ.
= inf{d(ξk∗ , y)|y ∈ X \O(π)} − δk
If Theorem 1 holds for φ, then as ρ(ξ ∗ , ¬φ, k) =
= ρ(ξ ∗ , π, k) − δk . −ρ(ξ ∗ , φ, k), we have −ρ(ξ ∗ , ¬φ, k) − δmax ≤
−ρ(ξ, ¬φ, k) ≤ −ρ(ξ ∗ , ¬φ, k) + δmax , thus
2) ξk∗ ∈
/ O(π), and [ξ k , ξ k ] ⊂ X \O(π), as shown in Fig. ρ(ξ ∗ , ¬φ, k) − δmax ≤ ρ(ξ, ¬φ, k) ≤ ρ(ξ ∗ , ¬φ, k) + δmax .
4 (b). In this case, for any ξk ∈ [ξ k , ξ k ], (iii) We assume that Theorem 1 holds for φ1 , φ2 and prove
ρ(ξ, π, k) = −inf{d(ξk , y)|y ∈ cl(O(π))}. Theorem 1 holds for φ1 ∧ φ2 .
If Theorem 1 holds for φ1 and φ2 , then ρ(ξ ∗ , φ1 , k) −
Thus from (11), we have δmax ≤ ρ(ξ, φ1 , k) ≤ ρ(ξ ∗ , φ1 , k) + δmax , ρ(ξ ∗ , φ2 , k) −
ρ(ξ, π, k) ≥ −inf{d(ξk∗ , y) + δk |y ∈ cl(O(π))} δmax ≤ ρ(ξ, φ2 , k) ≤ ρ(ξ ∗ , φ2 , k) + δmax . As ρ(ξ ∗ , φ1 ∧
φ2 , k) = min(ρ(ξ ∗ , φ1 , k), ρ(ξ ∗ , φ2 , k)), we have
= ρ(ξ ∗ , π, k) − δk .
min(ρ(ξ ∗ , φ1 , k), ρ(ξ ∗ , φ2 , k)) − δmax
3) ξk∗∈ O(π), but [ξ k , ξ k ] 6⊂ O(π), as shown in Fig. 4 ≤ ρ(ξ, φ1 ∧ φ2 , k)
(c). In this case, we have
≤ min(ρ(ξ ∗ , φ1 , k), ρ(ξ ∗ , φ2 , k)) + δmax ,
ρ(ξ, π, k) ≥ min ρ(ξ, π, k) = min{X1 , X2 },
ξk ∈[ξ ,ξ k ]
k
therefore ρ(ξ ∗ , φ1 ∧ φ2 , k) − δmax ≤ ρ(ξ, φ1 ∧ φ2 , k) ≤
where ρ(ξ ∗ , φ1 ∧ φ2 , k) + δmax .
(iv) We assume that Theorem 1 holds for φ and prove
X1 = − max inf{d(ξk , y)|y ∈ cl(O(π))},
ξk ∈[ξ ,ξ k ], Theorem 1 holds for φ1 UI φ2 .
k
ξk ∈O(π)
/ As
X2 = min inf{d(ξk , y)|y ∈ X \O(π)}.
ξk ∈[ξ ,ξ k ],
ρ(ξ ∗ , φ1 UI φ2 , k) = 0 max min ρ(ξ ∗ , φ2 , k 0 ),
k k ∈(t+I)
ξk ∈O(π)
∗ 00
min
00 0
[[φ 1 ]] (ξ , k ) ,
As d(ξk , y) ≥ 0, so X1 ≤ 0, X2 ≥ 0, min{X1 , X2 } = t≤kTherefore, it is proved by induction that Theorem 1 holds [18] N. Hoertel, M. Blachier, M. Olfson, M. Massetti, M. Rico, F. Limosin,
for any MTL formula φ. and H. Leleu, “A stochastic agent-based model of the SARS-CoV-2
epidemic in france,” Nature Medicine, vol. 26, pp. 1–5, 09 2020.
[19] E. Cuevas, “An agent-based model to evaluate the COVID-19 trans-
R EFERENCES mission risks in facilities,” Computers in Biology and Medicine, p.
[1] Z. Xu and U. Topcu, “Transfer of temporal logic formulas in rein- 103827, 2020.
forcement learning,” in Proc. IJCAI’2019, 7 2019, pp. 4010–4018. [20] P. C. Silva, P. V. Batista, H. S. Lima, M. A. Alves, F. G. Guimarães,
and R. C. Silva, “COVID-ABS: An agent-based model of COVID-19
[2] C. K. Verginis, C. Vrohidis, C. P. Bechlioulis, K. J. Kyriakopoulos, and
epidemic to simulate health and economic effects of social distancing
D. V. Dimarogonas, “Reconfigurable motion planning and control in
interventions,” Chaos, Solitons & Fractals, vol. 139, p. 110088, 2020.
obstacle cluttered environments under timed temporal tasks,” in 2019
[21] H. Inoue and Y. Todo, “The propagation of the economic impact
International Conference on Robotics and Automation (ICRA), May
through supply chains: The case of a mega-city lockdown to contain
2019, pp. 951–957.
the spread of COVID-19,” Covid Economics, vol. 2, pp. 43–59, 2020.
[3] Z. Xu, A. Julius, and J. H. Chow, “Energy storage controller synthesis
[22] S. L. Chang, N. Harding, C. Zachreson, O. M. Cliff, and
for power systems with temporal logic specifications,” IEEE Systems
M. Prokopenko, “Modelling transmission and control of the COVID-
Journal, Early access on IEEE Xplore.
19 pandemic in australia,” arXiv preprint arXiv:2003.10218, 2020.
[4] Z. Xu, B. Wu, and U. Topcu, “Control strategies for COVID-19
[23] N. Zheng, S. Du, J. Wang, H. Zhang, W. Cui, Z. Kang, T. Yang,
epidemic with vaccination, shield immunity and quarantine: A metric
B. Lou, Y. Chi, H. Long, M. Ma, Q. Yuan, S. Zhang, D. Zhang, F. Ye,
temporal logic approach,” PLOS ONE, vol. 16, no. 3, pp. 1–20,
and J. Xin, “Predicting COVID-19 in China using hybrid AI model,”
03 2021. [Online]. Available: https://doi.org/10.1371/journal.pone.
IEEE Trans. Cybernetics, vol. 50, no. 7, pp. 2891–2904, 2020.
0247660
[24] F. Liu, J. Wang, J. Liu, Y. Li, D. Liu, J. Tong, Z. Li, D. Yu,
[5] J. Weitz, S. Beckett, A. Coenen, D. David, M. Dominguez-Mirazo,
Y. Fan, X. Bi, X. Zhang, and S. Mo, “Predicting and analyzing the
J. Dushoff, J. Leung, G. Li, A. Magalie, S. Park, R. Rodriguez-
COVID-19 epidemic in China: Based on SEIRD, LSTM and GWR
Gonzalez, S. Shivam, and C. Zhao, “Intervention serology and interac-
models,” PLOS ONE, vol. 15, no. 8, pp. 1–22, 08 2020. [Online].
tion substitution: Modeling the role of ‘shield immunity’ in reducing
Available: https://doi.org/10.1371/journal.pone.0238280
COVID-19 epidemic spread,” Nature Medicine, pp. 849–854, 2020.
[25] B. M. Althouse, E. A. Wenger, J. C. Miller, S. V. Scarpino, A. Al-
[6] I. Cooper, A. Mondal, and C. G. Antonopoulos, “A sir model
lard, L. Hébert-Dufresne, and H. Hu, “Stochasticity and heterogene-
assumption for the spread of COVID-19 in different communities,”
ity in the transmission dynamics of SARS-CoV-2,” arXiv preprint
Chaos, solitons, and fractals, vol. 139, pp. 110 057–110 057, Oct
arXiv:2005.13689, 2020.
2020, 32834610[pmid]. [Online]. Available: https://pubmed.ncbi.nlm.
[26] A. Donze and V. Raman, “BluSTL: Controller synthesis from signal
nih.gov/32834610
temporal logic specifications,” in ARCH14-15. 1st and 2nd Interna-
[7] R. C. Reiner, R. M. Barber, J. K. Collins, P. Zheng, C. Adolph,
tional Workshop on Applied veRification for Continuous and Hybrid
J. Albright, C. M. Antony, A. Y. Aravkin, S. D. Bachmeier, B. Bang-
Systems, ser. EPiC Series in Computing, G. Frehse and M. Althoff,
Jensen et al., “Modeling COVID-19 scenarios for the united states,”
Eds., vol. 34. EasyChair, 2015, pp. 160–168.
Nature medicine, 2020.
[27] Z. Xu, F. M. Zegers, B. Wu, W. Dixon, and U. Topcu, “Controller
[8] J. M. Carcione, J. E. Santos, C. Bagaini, and J. Ba, “A simulation
synthesis for multi-agent systems with intermittent communication. a
of a COVID-19 epidemic based on a deterministic SEIR model,”
metric temporal logic approach,” in Allerton’19, pp. 1015–1022.
Frontiers in Public Health, vol. 8, p. 230, 2020. [Online]. Available:
[28] Z. Xu, K. Yazdani, M. T. Hale, and U. Topcu, “Differentially private
https://www.frontiersin.org/article/10.3389/fpubh.2020.00230
controller synthesis with metric temporal logic specifications,” in 2020
[9] Z. Feng, J. W. Glasser, and A. N. Hill, “On the benefits of
American Control Conference (ACC), 2020, pp. 4745–4750.
flattening the curve: A perspective,” Mathematical Biosciences, vol.
[29] S. Saha and A. A. Julius, “An MILP approach for real-time optimal
326, p. 108389, 2020. [Online]. Available: http://www.sciencedirect.
controller synthesis with metric temporal logic specifications,” in Proc.
com/science/article/pii/S0025556420300729
IEEE Amer. Control Conf., July 2016, pp. 1105–1110.
[10] X.-B. Zhang and X.-H. Zhang, “The threshold of a deterministic [30] Z. Xu, S. Saha, B. Hu, S. Mishra, and A. A. Julius, “Advisory temporal
and a stochastic SIQS epidemic model with varying total population logic inference and controller design for semiautonomous robots,”
size,” Applied Mathematical Modelling, vol. 91, pp. 749 – 767, 2021. IEEE Trans. Autom. Sci. Eng., pp. 1–19, 2018.
[Online]. Available: http://www.sciencedirect.com/science/article/pii/ [31] Z. Xu, A. A. Julius, and J. H. Chow, “Coordinated control of wind
S0307904X20305710 turbine generator and energy storage system for frequency regulation
[11] S. Zhao and H. Chen, “Modeling the epidemic dynamics and under temporal logic specifications,” in Proc. Amer. Control Conf.,
control of COVID-19 outbreak in China,” medRxiv, 2020. [Online]. 2018, pp. 1580–1585.
Available: https://www.medrxiv.org/content/early/2020/03/09/2020.02. [32] A. K. Winn and A. A. Julius, “Optimization of human generated
27.20028639 trajectories for safety controller synthesis,” in Proc. IEEE Amer.
[12] G. Giordano, F. Blanchini, R. Bruno, P. Colaneri, A. Di Filippo, Control Conf., June 2013, pp. 4374–4379.
A. Di Matteo, and M. Colaneri, “Modelling the COVID-19 epidemic [33] H. Abbas, A. Winn, G. Fainekos, and A. A. Julius, “Functional
and implementation of population-wide interventions in Italy,” Nature gradient descent method for metric temporal logic specifications,” in
Medicine, Jan. 2020. Proc. IEEE Amer. Control Conf., June 2014, pp. 2312–2317.
[13] B. Ivorra, M. Ruiz Ferrández, M. Vela, and A. Ramos, “Mathematical [34] Z. Xu, A. Julius, and J. H. Chow, “Optimal energy storage control
modeling of the spread of the coronavirus disease 2019 (COVID-19) for frequency regulation under temporal logic specifications,” in 2017
taking into account the undetected infections. The case of China,” American Control Conference (ACC), May 2017, pp. 1874–1879.
Commun Nonlinear Sci Numer Simul., April 2020. [35] G. E. Fainekos and G. J. Pappas, “Robustness of temporal logic spec-
[14] “Staggered release policies for COVID-19 control: Costs and benefits ifications,” in Formal Approaches to Testing and Runtime Verification,
of relaxing restrictions by age and risk,” Mathematical Biosciences, in: LNCS, vol. 4262, Springer, 2006.
vol. 326, p. 108405, 2020. [36] G. E. Fainekos and G. J. Pappas, “Robustness of temporal logic spec-
[15] S. Mwalili, M. Kimathi, V. Ojiambo, D. Gathungu, and R. Mbogo, ifications for continuous-time signals,” Theoretical Computer Science,
“SEIR model for COVID-19 dynamics incorporating the environment vol. 410, no. 42, pp. 4262 – 4291, 2009.
and social distancing,” BMC Research Notes, vol. 13, no. 1, p. 352, [37] R. Elie, E. Hubert, and G. Turinici, “Contact rate epidemic control of
2020. COVID-19: an equilibrium view,” 04 2020.
[16] S. Alonso-Quesada, M. De la Sen, R. Agarwal, and A. Ibeas, “An [38] A. Schrijver, Theory of Linear and Integer Programming. John Wiley
observer-based vaccination control law for a SEIR epidemic model & Sons, Chichester, 1986.
based on feedback linearization techniques for nonlinear systems,” [39] L. Beal, D. Hill, R. Martin, and J. Hedengren, “Gekko optimization
Advances in Difference Equations, vol. 2012, 09 2012. suite,” Processes, vol. 6, no. 8, p. 106, 2018.
[17] M. d. R. de Pinho, I. Kornienko, and H. Maurer, “Optimal control of a [40] M. Althoff, “An introduction to cora 2015,” in ARCH14-15. 1st and
SEIR model with mixed constraints and L1 cost,” in CONTROLO’2014 2nd International Workshop on Applied veRification for Continuous
– Proceedings of the 11th Portuguese Conference on Automatic and Hybrid Systems, ser. EPiC Series in Computing, G. Frehse and
Control, A. P. Moreira, A. Matos, and G. Veiga, Eds. Cham: Springer M. Althoff, Eds., vol. 34. EasyChair, 2015, pp. 120–151.
International Publishing, 2015, pp. 135–145.You can also read