Polyatomic Molecules as Quantum Sensors for Fundamental Physics
←
→
Page content transcription
If your browser does not render page correctly, please read the page content below
Polyatomic Molecules as Quantum Sensors for
Fundamental Physics
Nicholas R. Hutzler
arXiv:2008.03398v1 [physics.atom-ph] 7 Aug 2020
California Institute of Technology
Division of Physics, Mathematics, and Astronomy
Pasadena, CA 91125
E-mail: hutzler@caltech.edu
August 2020
Abstract. Precision measurements in molecules have advanced rapidly in recent
years through developments in techniques to cool, trap, and control. The complexity
of molecules makes them a challenge to study, but also offers opportunities for
enhanced sensitivity to many interesting effects. Polyatomic molecules offer additional
complexity compared to diatomic molecules, yet are still “simple” enough to be laser-
cooled and controlled. While laser cooling molecules is still a research frontier itself,
there are many proposed and ongoing experiments seeking to combine the advanced
control enabled by ultracold temperatures with the intrinsic sensitivity of molecules. In
this perspective, we discuss some applications where laser-cooled polyatomic molecules
may offer advantages for precision measurements of fundamental physics, both within
and beyond the Standard Model.Polyatomic Molecules as Quantum Sensors for Fundamental Physics 2
1. Introduction full quantum control [5]. One critical differ-
ence compared to diatomic molecules [15] is
Atoms and molecules can serve as sensitive that polyatomics, by which we mean molecules
probes of essentially every particle, force, and with three or more atoms, have additional me-
interaction – both known and unknown [1]. chanical degrees of freedom – they can rotate
From measuring gravity to searching for su- and vibrate in many ways. How these addi-
persymmetry, atoms and molecules make pro- tional degrees of freedom can benefit precision
found contributions to our understanding of measurements is the focus of this perspective.
the universe, often using experiments that can First, we begin with a very brief introduc-
fit on a (possibly large) table. An important tion to the relevant properties of polyatomic
advantage is the availability of techniques to molecules, including their multiple degrees of
control their degrees of freedom, both clas- freedom, and the ability to generically polar-
sical and quantum, and make measurements ize them in small electric fields. Next, we dis-
with extreme precision. In this perspective we cuss some aspects of laser cooling molecules,
will focus on an emerging area – laser-cooled and how these techniques are applicable to
polyatomic molecules – and the contributions polyatomic species. Finally, we describe some
which they could make to fundamental physics. searches for fundamental physics which could
Molecules are of interest not just for their benefit from the unique features of polyatomic
applications to fundamental physics [1, 2, 3, 4], molecules, in particular those which can be
but also to quantum chemistry [5, 6], quantum laser-cooled.
matter [6, 7], quantum information [8], and
more. Their complexity is a powerful feature;
2. Polyatomic Molecules
they have more states, more energy scales,
more interactions, and more interacting bodies The structure of polyatomic molecules is fan-
compared to atoms. Complexity is not always tastically complex and diverse, so here we will
better, as it makes them difficult control only describe the features critical to under-
and understand, but advances in experimental standing the experiments that we discuss [16,
and theoretical techniques have started to 17, 18]. A discussion of some important fea-
make possible many of the exciting promised tures of diatomic molecules can be found in the
applications. Advanced methods to cool and appendix. The first main difference relative
control molecules, including laser cooling [9, to diatomics is that polyatomic molecules have
10], promise a revolution in molecular science multiple vibrational degrees of freedom. The
like they did for atomic science. vibrational state is often specified as (ν1 . . . νn ),
The additional internal degrees of freedom where νi is an integer counting the number of
and chemical diversity of polyatomic molecules quanta in the ith mode. For example, a linear
make them a promising platform for many triatomic of the form MOH, where M is much
areas of research. In this perspective we heavier than O, has three modes: M–O stretch,
will focus on fundamental physics, but poly- M–O–H bend, O–H stretch, which are typically
atomic molecules also have specific advan- denoted as modes 1, 2, 3, respectively.
tages for quantum information and many-body Bending modes of a linear bond are
physics [11, 12, 13, 14], and give many more doubly-degenerate since the bending can
chemical bonds and reactions to study with occur in either of two perpendicular planes.Polyatomic Molecules as Quantum Sensors for Fundamental Physics 3
Superpositions of these two modes with a distinct moment of inertia, are also of interest
phase difference correspond to states where and all of the advantages we shall discuss
the middle nucleus is orbiting around the generally apply to them as well [21], though
symmetry axis with angular momentum `, as we will not consider them specifically here.
though it was a permanently bent molecule
rotating around its symmetry axis. States 2.1. Parity doubling and polarization
with well-defined ` are not parity eigenstates
Parity doublets are a useful resource since they
since reflection will interchange +` ↔ −`,
enable polarization in small electric fields. The
so in free space the eigenstates are equal
electric dipole operator d~ = e~r is parity-odd,
superpositions |+`i ± |−`i. These states have
and any parity eigenstate |ψi must therefore
opposite parity and are split by an amount ~
have a dipole moment of zero: hψ|d|ψi =
called the `−doubling, typically tens of MHz.
0. Since parity is a symmetry of free
This is similar in many respects to Λ-doubling
space (to good approximation), atomic and
(see the appendix), and we shall consider it in
molecular eigenstates are parity eigenstates
more detail later. Therefore, each rotational
in the absence of applied fields. Non-zero
level in these vibrational states is split into
dipole moments therefore arise as a result of
two states of opposite parity, as opposed to a
mixing states of opposite parity, for example
ladder of rotational states with a well-defined, ~ The small
by applying a static electric field E.
alternating parity when these doublets are
splitting of parity doublets makes this happen
absent. States which can support vibrational
at lower fields.
angular momentum include a superscript ` in
As an example, consider a two level
their state labels, such as (ν1 ν2` ν3 ) for a linear
system split by energy ~∆ with states coupled
triatomic (though this is often omitted for
by an electric field E,
ν2 = 1, as there is only one possible value of !
`). −~∆/2 −dE
H= .
An important type of non-linear molecule −dE +~∆/2
is the symmetric top, which has three non- The energies of this system are given by
zero moments of inertia but with two of them 1 1/2
E± = ± ~∆ 1 + 4η 2
equal (unlike a linear molecule, which has two ,
2
moments of inertia equal and one vanishing) where we have defined η ≡ |dE|/~∆. At
such as NH3 or CaOCH3 . These molecules very high fields, η
1, we obtain the usual
have additional rotational structure due to linear Stark shift E± ≈ ±dE, whereas at
rotation about the symmetry axis, quantized low field we obtain quadratic shifts ∆E± ≈
by the number K. States with ±K rotational d2 E 2 /~∆, as shown in figure 1. This is the
quanta about the symmetry axis are nominally characteristic behavior of an induced dipole,
degenerate, but like `-doubling the field-free where the degree of polarization P is
eigenstates are even and odd superpositions
∂E± 2η
of ±K with opposite parity. These K- P = =p .
∂(dE) 1 + 4η 2
doublets are split by an amount even smaller
than `−doublets, typically .1 MHz for the The scale of the cross-over point from
types of molecules considered here [19, 20]. linear to quadratic is η ≈ 1, or ~∆ ≈
Asymmetric top molecules, which have three dE. Therefore, the field required to polarizePolyatomic Molecules as Quantum Sensors for Fundamental Physics 4
non-zero electronic orbital angular momentum,
�
c
drati
Qua
�� as well as other sources of doubling such as
Linear
tunneling (the classic example being NH3 [16]),
��
� are always split by some small amount. The
specific origin is different for every source of
doubling, but often involves the rotation of the
molecule. For example, the non-linearity in
a bending mode reduces the symmetry of the
molecule as it can be viewed as a bent molecule
rotating around its symmetry axis. This
lifts the degeneracy of the moments of inertia
Figure 1. Stark shifts and polarization in a model about axes perpendicular to the symmetry
two level system. Top: The actual shifts (thick solid axis, resulting in slightly different energy for
lines) transition from quadratic at low field to linear the nominally degenerate bending modes as
at high field, with a cross-over point where |dE| ≈
the molecule rotates.
~∆. The states with linear shifts correspond to the
molecular dipole polarized in the lab frame in one of There is a more qualitative argument
two directions. This pair of states with equal-and- to understand why states with Λ, `, and
opposite polarization is unique to systems with parity K doublets can be easily polarized, and
doublets. Bottom: Polarization is linear at low fields arises from the fact that they all are non-
as the molecules have an induced dipole, and saturates
at high fields as the dipole becomes fully induced.
zero angular momentum projections on the
internuclear axis n̂, along which the molecular
dipole points [22]. Consider a molecule with
something reduces linearly with the splitting ` > 0 (the cases for Λ, K are similar) and
of opposite parity states. A typical, atomic rotation R ~ ⊥ n̂, as shown in figure 2.
unit of dipole moment ea0 translates to an These angular momenta are coupled via the
energy shift of ≈1 MHz in 1 V/cm of rotational interaction described in the previous
electric field. Atoms must mix opposite parity paragraph, or more generally Coriolis-type
electronic states, and are therefore limited forces, so the total angular momentum J~ =
to P ≈ η ≈ 10−3 even in large fields of ~` + R ~ is the only good vector in the lab
∼100 kV/cm, whereas molecules can achieve frame. Accordingly, since the molecular dipole
P ∼ 1 by mixing rotational states in fields moment d~ ∝ n̂ ∝ ~`, we have that d~ · J~ 6= 0.
of ∼10 kV/cm, or by mixing parity doublets The non-zero projection of the dipole moment
in fields of . 1 kV/cm (even as low as along a good, lab-frame quantum number
1 V/cm). Besides becoming polarized at means that there is a linear dipole moment
smaller fields, the availability of states with in the lab frame, and in fact this projection
equal-yet-opposite polarization has important argument even gives the correct magnitude of
implications which will be explored later. the effect. Of course this argument ignores the
Unfortunately, this splitting ∆ is never fact that the ±` states are split, but intuitively
zero [19], so molecules always have induced captures the importance of angular momentum
dipole moments. The sources of doubling projections on the internuclear axis. States
mentioned above (` and K), along with the with no angular momentum projection along
Λ or Ω doubling present in molecules with the internuclear axis, for example 2 Σ linearPolyatomic Molecules as Quantum Sensors for Fundamental Physics 5
molecules, correspondingly do not have linear been observed, and could only arise from
Stark shifts, and even when fully polarized exotic symmetry-violating physics as we shall
do not possess pairs of states with equal and discuss later. Objects frequently claimed
opposite polarization. to have permanent electric dipole moments,
such as H2 O, NH3 , NaCl, etc. in fact
J R
have induced dipole moments. These polar
molecules transition from the quadratic to
d·J the linear Stark regime in “very small” fields,
�
� but have quadratic Stark shifts at sufficiently
d small fields indicative of induced dipoles.
The earlier discussion about parity proves
that this must always be the case, but the
physical chemistry behind why this happens
� in molecules is also understood [19, 20]. The
confusion is compounded by the fact that the
quantity d is usually called the permanent
Figure 2. The importance of angular momenta with dipole moment of the molecule, since it can be
non-zero projection on the internuclear axis n̂. Top: viewed as the dipole moment in the molecular
For a molecule (shown as diatomic for simplicity) where
frame. However, the molecular frame is a
the total angular momentum J~ has non-zero projection
on the internuclear axis, J~ · n̂ 6= 0, the projection of mathematical construct (albeit a physically
the molecule-frame dipole moment on J~ is non-zero, intuitive one) and only the dipole moment in
J~ · d~ 6= 0. This occurs whenever there is some angular the lab frame is physically observable, and
momentum quantized along n̂, which can arise from must be aligned by application of fields.
electronic or mechanical means. Since J~ is a good
vector in the lab frame, the result is a linear Stark shift.
Bottom: Angular momentum along the symmetry axis 3. Laser Cooling
can , for example, due to rigid body rotations (left)
bending (right). Laser cooling molecules has advanced with
tremendous speed, from the first demonstra-
Parity doublets are already of impor- tion in 2010 [26] to the implementation of ad-
tance in diatomic molecular precision mea- vanced cooling and trapping techniques in re-
surements [23, 24, 25], where they arise as cent years. Many of these developments are
a result of Λ or Ω doubling. However, the the topic of recent reviews [9, 10], and we will
generic availability of parity doublets in poly- not repeat this very interesting story or sum-
atomic molecules is largely independent of elec- marize the results of the field here, apart from
tronic structure. Much of what we discuss those directly relevant to our topics. Instead,
here will depend on some particular electronic we will briefly review some of the key features
structure, such as laser cooling and sensitivity and challenges of laser cooling diatomic and
to fundamental symmetry violations, so poly- polyatomic molecules.
atomic molecules offer new opportunities to The motivation for laser cooling and trap-
combine these features. ping in precision measurements is extremely
As an aside, it is important to note strong. Ultracold and trapped species can offer
that no permanent dipole moment has ever long coherence times, large numbers, precisePolyatomic Molecules as Quantum Sensors for Fundamental Physics 6
control of electromagnetic environments, and thereby reducing (though not eliminating) the
the opportunity for advanced quantum control role of uncontrolled spontaneous decay.
and engineering [27, 28, 29]. The potential gain One key ingredient to the solution is to
in sensitivity is orders of magnitude for many find molecules unlikely to change their vi-
interesting sources of new physics, including brational state during an electronic decay, of
those that we will consider in the next sec- which there are actually a fair number [41].
tions. For example, searches for fundamental As long as the potential energy surface (PES)
symmetry violation utilizing all of these advan- of the ground |gi and excited states |ei have
tages could probe energy scales far outside the a similar shape, the molecule is unlikely to
reach of any particle accelerators, and several change its vibrational state during a decay [22].
are already underway [29, 30, 31, 32, 33, 34]. This is because, to good approximation, the
We will consider laser-cooled neutral molecules electronic transition is instantaneous com-
here, though techniques with trapped molecu- pared to the vibrational motion of the molecule
lar ions offer another route to major improve- (Born-Oppenheimer approximation), so the vi-
ments without relying on laser cooling [24, 35]. brational wavefunction |vi is diabatically re-
The basic idea of laser cooling molecules projected onto the eigenstates of the new PES.
is identical to that of atoms [36], and in This is quantified by the Franck-Condon fac-
its most common form relies on repeatedly tors (FCFs) of the electronic transition, qv0 v =
exciting an electronic transition with a laser so |he, v 0 |g, vi|2 . If the two PESs are identical then
that photons are scattered from the molecule. qv0 v = δv0 v , the vibrational wavefunction will
This “photon cycling” transfers momentum not change (within this approximation), and
to the molecule, and can be engineered to this transition is said to be “diagonal” as the
apply dissipative forces which cool toPolyatomic Molecules as Quantum Sensors for Fundamental Physics 7
A�� v =0 p state, resulting in an electronic wavefunction
which is pushed away from the chemical bond,
as shown in figure 4. The excited p state can
q 0v
similarly hybridize with d states, and is alsoPolyatomic Molecules as Quantum Sensors for Fundamental Physics 8
demonstrated in 2017 with SrOH [49]. This technique used by current molecular laser
relative insensitivity to the ligand means cooling experiments is the cryogenic buffer
that the ligand itself can contain something gas beam (CBGB) [64, 65], which uses an
interesting, for example another cycling center, inert gas in a cryogenic environment (typically
or an atom with some desirable property which helium around 2 − 5 K) to create cold, slow,
cannot be laser-cooled itself [50, 51, 52, 53]. and intense beams of essentially any species,
This also means that the polyatomic analogue including molecular radicals suitable for laser
will generally maintain other useful properties cooling.
of the diatomic electronic structure, such Molecules which have been laser slowed,
as sensitivity to the fundamental symmetry cooled, and trapped in 3D are limited to the
violations [54] to be discussed later. diatomic species SrF [42], CaF [62, 66], and
So far we have discussed only vibration, YO [67]. The diatomic molecules YbF [33] and
but rotation plays an important role in BaH [68] have been laser-cooled, but not yet
molecular laser cooling as well. Because trapped. Laser-cooled polyatomic molecules
rotational level changes must follow selection include SrOH [49], CaOH [69], YbOH [56],
rules due to parity and conservation of and CaOCH3 [63], with a large number of
angular momentum, unlike vibrational level proposed other species which could be cooled
changes‡, the number of potential rotational using these methods [21, 45, 47, 48, 52, 53, 54].
loss channels is limited – decays can only occur Even in the short time that these systems
to states of opposite parity, and satisfying have been available, many advanced cooling
∆J ≤ 1. However, rotational state-changing and trapping methods have been implemented
decays can be eliminated through clever such as magnetic trapping [10, 70, 71], optical
application of the selection rules with highly trapping [72], application of spontaneous
non-trivial consequences [58]. We will not go forces [38], tweezer trapping [73], and a variety
into the details of the idea, or experimental of sub-Doppler cooling methods [49, 63, 66, 56,
implementation [9, 10, 58, 59, 60, 61, 62], 71, 72, 74, 75] to reach temperatures as low as
largely because the solutions are quite general. 5 µK.
However, we will point out that non-linear There are other methods to directly cool
molecules present additional challenges due molecules to ultracold temperatures, for exam-
to their more complex rotational structure, ple sympathetic [76, 77], evaporative [78, 79],
though these challenges can be addressed as or optoelectrical [80, 81] cooling. These meth-
well [48, 21, 63]. ods do not rely on the availability of closed cy-
Rotational structure is also important cling transitions, and are therefore applicable
because it necessitates efficient pre-cooling. to a different set of species. Additionally, tech-
Thermal sources on the order of ∼ 1, 000 K niques for precision measurement and control
would disperse the molecule population over using trapped molecular ions [35, 82, 83] enable
hundreds or thousands of internal states, since very sensitive measurements without the need
rotational energy scales are ∼ 1 K. The for laser cooling. Other approaches relevant
‡ There are selection rules regarding vibrational
for precision measurement involve formation of
angular momentum, which reduces the number of ultracold atoms into ultracold molecules [84],
states needing to be re-pumped in a linear molecule, and trapping molecules in gas matrices [85].
though they are not strictly obeyed [55, 56, 57].Polyatomic Molecules as Quantum Sensors for Fundamental Physics 9
4. Fundamental Symmetries this new physics via virtual, radiative correc-
tions, similar to how the electron’s magnetic
We now shift to discussing our first application moment is influenced by quantum electrody-
of laser-cooled polyatomic molecules to study namics through virtual couplings to photons
fundamental physics. We will consider and positrons. These couplings will alter the
two areas where polyatomic molecules offer electromagnetic properties of the particles, and
some unique advantages – the search for imbue them with symmetry-violating electro-
undiscovered sources of CP-violation, and the magnetic interactions that can only arise due
precision study of P-violation by the weak to exotic symmetry violating physics.
nuclear force. Molecules are already playing The classic example is a permanent
an important role in studying fundamental electric dipole moment (EDM). For a particle
symmetries and their violations, and we refer with spin ~s, the EDM d~ must be aligned along
the reader to some recent reviews for detailed the spin, d~ ∝ ~s. This is a consequence of the
discussions [1, 2, 3, 4]. Wigner-Eckart theorem, or more intuitively,
because the EDM is a vector quantity and spin
4.1. CP-violation is a particle’s only internal vector quantum
The observed imbalance between matter and number. This is empirically verified by
anti-matter in the universe cannot be ex- quantum statistics; the indistinguishability of
plained [86]. According to all known physics, particles gives rise to the unique features of
the properties of matter and anti-matter are atomic and nuclear structure, which are a
essentially identical, including how they could consequence of the fact that intrinsic spin is
be produced after the big bang. The ab- the only internal vector describing electrons
sence of free anti-matter in the universe there- and nucleons. The very existence of a
fore suggests some undiscovered fundamen- permanent EDM therefore violates a number
tal symmetry violating process. One of the of fundamental symmetries as d~ and ~s behave
symmetries violated by this process, in ad- oppositely under parity (P) and time (T)
dition to a preference of matter over anti- reversal, and also CP by the theorem that the
matter, is the simultaneous inversion of charge product CPT is always conserved [88]. This
and parity, or CP [87]. While this symme- relates to our earlier discussion that permanent
try is violated in the Standard Model via the EDMs do not exist normally, but only arise as
weak force CKM mechanism, its effects are a result of exotic CP-violating physics.
sufficiently suppressed so that it cannot ex- The signatures of these moments can be
plain the matter-dominated universe. There significantly enhanced by the large internal
is therefore strong motivation to search for electromagnetic fields and gradients present in
undiscovered CP-violating physics, and it is atoms and molecules, especially species with
a major driver of research in many areas of a heavy nucleus, and are many orders of
physics [1, 3, 88, 89, 90]. magnitude larger than what is achievable with
Despite their high energy origin, these ef- laboratory fields. The constituent electrons
fects can manifest themselves as low energy and nuclei experience these large fields in
observables. Regular, Standard Model parti- their bound states, giving rise to symmetry-
cles like electrons and neutrons can couple to violating energy shifts. For example, the
electron EDM gives rise to a molecular energyPolyatomic Molecules as Quantum Sensors for Fundamental Physics 10
shift Hedm = −de Eeff S ~ · n̂, where S
~ is the of polarization P defined earlier. This fact
effective total valence electron spin, Eeff is is the principle reason why molecules have
the effective electric field experienced by the increased sensitivity compared to atoms; the
electrons, and n̂ is the internuclear axis, along internal fields are actually very similar in
which the internal electric field must point. both atoms and molecules, as they depend
Eeff scales very rapidly with proton number, almost entirely on the short-range electronic
roughly as Z 3 , and is ∼10-100 GV/cm for wavefunction near the nucleus [92]. Thus
the molecules discussed here, much larger the ability to achieve O(1) polarization in
than macroscopic fields that can be realized molecules, as discussed earlier, is the source
in the lab. This gives rise to energy shifts of their advantage over atoms.
∝ ±M ∝ ±MS , the projection of the Molecules with parity doublets offer the
total angular momentum M , which includes additional advantage of polarization in much
the total electron spin MS . This is shown smaller fields. This simplifies engineering, but
schematically in figure 5. also reduces many important systematic effects
These energy splittings are generally too which are proportional to the electric field [93].
small to observe directly, for example by Another critical feature afforded by parity
looking for a shift in a spectral line, so doublets is the “internal co-magnetometer,”
instead the Ramsey method of coherent spin or ability to reverse the EDM signal without
precession is used [88]. By creating a changing applied fields at all [23]. A fully
superposition of the ±M levels, the phase polarized molecule with parity doublets yields
difference between them will build up linearly two (nearly)-identical level structures with
in time as long as the system remains coherent, opposite Stark shifts, corresponding to the
leading to a sensitivity ∝ τ N 1/2 , where τ is different orientations of the molecule n̂, and
the coherence time and N is the total number therefore opposite EDM shifts, as shown in
of measurements. Laser cooling offers the figure 5. This gives significant robustness
ability to improve coherence times by orders against systematic effects resulting from field
of magnitude compared to the current best non-uniformity and imperfect reversals, and
measurements with neutral molecules [25, 91], is a critical component of the most sensitive
which have τ ≈ 1 ms, while maintaining current eEDM experiments [24, 25].
large molecule numbers. However, this is not Since diatomic parity doubling occurs
the only method to achieve long coherence only from Λ-doubling in states with Λ > 0,
times, as they are already being realized in this rules out the types of laser-coolable di-
molecular ion trap EDM searches without laser atomic molecules discussed earlier with metal-
cooling [24, 35]. centered s electrons. However, the parity
We can infer from the previous discussion doubling generically present in polyatomic
that the species must be polarized for the molecules can be used to bypass these prob-
EDM shifts to be non-zero. This can be lems [29]. Since doubling in polyatomics can
seen from the EDM Hamiltonian ∝ S ~ · n̂; occur as a result of mechanical motion of the
an unpolarized molecule has hn̂i = 0 so the nuclei, as opposed to electronic motion, we
energy shifts will average away in the lab can design molecules with a desirable elec-
frame. Electrically polarizing the species gives tronic structure, such as laser cooling and good
a non-zero average n̂ proportional to the degree CP-violation sensitivity [54], and include par-Polyatomic Molecules as Quantum Sensors for Fundamental Physics 11
this method [29, 94, 95].
Heavy
Metal
d
4.1.1. Electron electric dipole moment.
e - eff Diatomic molecules are currently the most
sensitive platform to search for the electron
Ligand EDM, with YbF [91], ThO [25, 96], and
HfF+ [24] surpassing the most sensitive atomic
experiment performed using Tl [97]. The
d≠0 current limit of |de | < 1.1 × 10−29 e cm is
d=0 ~d eff
set by the ACME experiment using ThO [25],
e-
e- which is already ruling out new CP-violating
particles with masses . 10 TeV, exceeding the
reach of particle accelerators and constraining
interesting new physics theories such as
supersymmetry and models of baryogenesis [1,
25, 98]. Each of these diatomic experiments is
also implementing improvements to continue
pushing their sensitivity [33, 35, 99, 100, 101].
There are also a number of diatomic molecules
e- e- with high sensitivity to the electron EDM
which can be laser-cooled, including BaF [102],
Figure 5. Energy shifts due to an electron EDM, YbF [28, 33, 35], HgF [103], and RaF [104,
though the idea is applicable for NSM and MQM shifts 105], all of which have the structure of a metal-
as well. Top: The valence electrons in a molecule centered s electron giving rise to a 2 Σ state
experience very large internal fields, especially near
described earlier.
the nucleus of a heavy metal. Middle: The eEDM
interacts with the internal field and gives rise to Polyatomic molecules with 2 Σ electronic
symmetry-violating energy shifts, for example between ground states are promising candidates to
the electron spin up and down states. Bottom: In combine laser cooling, large values of Eeff ,
a molecule with parity doublets, there are two pairs
and parity doublets in the same system [29].
of Stark-shifted spin up/down states, one for each
orientation of the fully polarized molecule. By combining long coherence times, large
numbers, and robustness against systematics,
eEDM limits can be improved by orders
ity doublets arising from largely independent of magnitude, exceeding the reach of even
degrees of freedom. The bending modes in conceivable particle accelerators. So far, the
linear molecules (`−doubling) or the rotation effective electric field has been computed for
of symmetric tops about their symmetry axis many molecules of the form MOH, where
(K−doubling) considered earlier are present M=Ca, Sr, Ba, Yb, Hg, and Ra [54,
in laser-coolable molecules, and offer high 106, 107, 108, 109]. As expected, their
polarizability and internal co-magnetometers. sensitivities are comparable to their diatomic
Additionally, these doublets enable precision analogues. An experimental effort to search
molecular ion trap measurements, and there- for the electron EDM using laser-cooled YbOH
fore opens a number of interesting species to molecules is underway [29, 56, 110, 111, 112,Polyatomic Molecules as Quantum Sensors for Fundamental Physics 12
113], as is spectroscopic exploration of other fundamental particles and forces in the
candidate Yb-containing molecules such as hadronic sector, including nucleon dipole
YbOCH3 [114]. moments and CP-violating nuclear forces [1,
98]. Other atomic searches include Ra [30,
4.1.2. Nuclear CP-violation. CP-violation 121], Xe [122, 123], and Rn [124]. Molecular
can also occur in the nucleus, and manifest searches include TlF [27, 31, 125, 126] and
as a nuclear Schiff moment (NSM) or nuclear RaF [104, 105, 127], both of which can
magnetic quadrupole moment (MQM). Both be laser-cooled. RaF and Ra have a
are sensitive to physics active in the nucleus, further enhancement due to an octupole (β3 )
as opposed to that which couples to the deformation of the Ra nucleus [119, 128],
electron, and are therefore largely orthogonal leading to an intrinsic Schiff moment & 1000
and complementary to eEDM searches. NSMs times larger than in spherical nuclei such as
and MQMs arise, for example, from nucleon Hg.
EDMs, new CP-violating nuclear forces, strong Another nuclear CP-violating moment is
force CP-violation (θ, discussed again later), the magnetic quadrupole moment (MQM),
and more [1, 3, 98, 115, 116]. which arises due to the same physics sources
A point-like nucleus with an EDM would as the NSM but as a magnetic instead of
not interact with internal electric fields since electric effect [88, 115, 118, 129] and with
the charged nucleus would, in steady-state, different relative sensitives to the sources [130].
move to a position where it experienced zero In a single particle picture, the orbiting
average field and therefore no forces. A valence nucleons in a nucleus will result in
nuclear dipole moment therefore appears to be an MQM if they have EDMs, as a rotating
unobservable in an atom or molecule, which EDM creates an MQM. The orientation of
is known as Schiff’s theorem§. However, the the MQM is determined by the nuclear spin
nucleus is not a point, and the fields are not I, which violates CP. The MQM will interact
“screened” perfectly, resulting in a residual with valence electrons to induce an EDM in
electric interaction called the Schiff moment, the species, which can be distinguished from
~ ∝ I,
S ~ and giving rise to an energy shifts the eEDM by its hyperfine dependence [118,
∝ S · n̂ ∝ I~ · n̂, where I~ is the nuclear spin. The
~ 130]. Since the MQM is not screened,
NSM therefore behaves similarly to a nuclear the effect is typically larger in heavy nuclei
dipole moment interacting with an internal compared to the NSM. The single-nucleon
electric field, but depends very strongly on picture underestimates the MQM, which is
the structure of the nucleus. The effect scales enhanced by collective effects in quadrupole-
roughly with proton number as ∼ Z 2 , but deformed (β2 ) nuclei by around an order of
can be enhanced by orders of magnitude in magnitude [130, 131]. Because both the NSM
deformed nuclei [118, 119]. and MQM could arise due to a large number of
The most sensitive current search for a physics sources, measurements of these effects
NSM is the 199 Hg vapor cell experiment [120], in multiple species complement each other [98,
and is probing the ∼ 10 TeV scale for 130, 132].
The experimental procedure and require-
§ This theorem applies to the electrons equally well,
but is evaded by the fact that the electron is moving ments of NSM and MQM experiments are very
relativistically [117]. similar to those for eEDM, in particular thePolyatomic Molecules as Quantum Sensors for Fundamental Physics 13
requirement for polarization. This means that the electrons with the nucleus, and results in
the parity doublets of polyatomic molecules are the mixing of opposite parity states in species
a useful resource, and again do not in general with core-penetrating s1/2 or p1/2 electrons.
interfere with the electronic structure require- This mixing leads to PV transition amplitudes
ments for good sensitivity. NSM sensitivity between opposite-parity states in atoms and
has been examined for a number of species, in- molecules. Only one experiment has managed
cluding TlCN [133], RaOH [54], RaOH+ , and to observe an AM [139], though others are un-
ThOH+ [94], along with MQM sensitivity for derway [1]. Anapole moments are an impor-
BaOH [134], LuOH+ [135], and YbOH [134, tant tool for studying the weak nuclear force
136], which is being pursued for an MQM at low energies and in the hadronic sector [140],
search in a molecular beam [29, 110, 113]. All and are sensitive probes for new fundamental
of these sensitivities, like Eeff , have so far been physics [141], making complementary measure-
quite similar to their fluoride analogues. ments in diverse systems very desirable.
This mixing of opposite-parity gives
4.2. Parity violation molecules a distinct advantage. The mixing is
enhanced when the states are closely-spaced,
While CP-violation is yet to be observed in
and molecules have opposite parity states with
atoms or molecules, another important sym-
much smaller spacing compared to atoms. In
metry violation, parity (P), has been observed
addition, these states can be pushed to near-
in a few [1, 137]. The effects of the weak
degeneracy using magnetic fields [142, 143,
nuclear force on nuclei and electrons results
144, 145], as shown in figure 6. The PV
in symmetry-violating effects such as mixing
amplitude can be measured by observing its
of opposite parity states. While these ef-
interference with the electric dipole-allowed
fects are extremely small, they can be dis-
component of the transition due to their
tinguished from purely electromagnetic effects
different interactions with applied electric
through their symmetry-violating characteris-
fields. This method has now been refined to
tics. There are a number of parity violating
the point where it has demonstrated statistical
(PV) effects present in atoms and molecules,
and systematic sensitivity that should enable
and several methods of measurement, though
a measurement of the 137 Ba AM using the BaF
we only discuss one where molecules have a
molecule with ∼ 10% precision [146].
particular advantage – nuclear spin-dependent
The expanded availability of opposite-
(NSD) PV and anapole moments [1, 137].
parity levels in polyatomic molecules leads
The anapole moment (AM) [138] is a
to further enhancements of this method [145,
NSD PV effect arising from W and Z bosons
148]. Diatomic molecules in 2 Σ states (such
exchanging between nucleons in the nucleus
as in BaF [146]) require large magnetic fields
and modifying the electron-nucleus interac-
to push rotational states into degeneracy,
tion. This effect is equivalent to the nucleus
which are spaced by several GHz, whereas the
possessing a toroidal current distribution, like
parity doublets in polyatomic molecules are
a solenoid curved into a torus, whose orienta-
smaller by orders of magnitude. Molecules of
tion is determined by the nuclear spin. Since
the form MOH, MNC, and MCN [145, 148]
a toroidal magnetic field has no effects at
for M=Be, Mg, Ca, Sr, Ba, Yb, and Ra,
long range, the AM is a contact interaction of
for example, have parity doublets in theirPolyatomic Molecules as Quantum Sensors for Fundamental Physics 14
Energy � the sensitivity scales with number and coher-
Enhaced Static PV � ence time similar to CP-violation searches, op-
tical trapping or molecular fountains should
lead to orders-of-magnitude improvement in
sensitivity. Such an experiment is currently
Enhanced under development [145].
Oscillating PV This approach gives an extremely wide
� Magnetic Field range of nuclei to probe, from the very light
to the very heavy. While heavy nuclei are
Figure 6. Enhancement of parity-violating (PV)
mostly sensitive to the AM, which scales
effects in polyatomic molecules. Parity-doubled states
can have roughly quadratic or linear Zeeman shifts roughly as A2/3 where A is the mass number,
due to hyperfine coupling, leading to tunable energy lighter nuclei are sensitive to multiple sources
spacings. When these states intersect, static PV effects of NSD PV with smaller magnitudes and
are enhanced [145]. When the splitting is resonant with are easier to benchmark against calculations.
the oscillation frequency of an axion-like particle (see
section 5.2) oscillating PV effects are enhanced [147].
The increased sensitivity of the polyatomic
Note that there are many other levels and crossings not approach is a compelling way to measure these
shown for simplicity. effects in a wide range of nuclei [148], as
well as search for new effects such as the
excited bending states which enable near- weak quadrupole moment [149], which would
degeneracies in fields of .100 G, compared to enable measurements of neutron distributions
thousands of G for comparable diatomics [144]. in nuclei.
In addition to being technically easier, this
reduces systematic effects related to the fields, 4.2.1. Parity-violating energy shifts. The
as well as broadening of the transition due to weak nuclear force also results in energy
field non-uniformities. shifts between different enantiomers of chi-
Opposite-parity states within a rotational ral molecules, though this is yet to be ob-
manifold which can be pushed into degener- served experimentally due to its extremely
acy at small fields are fairly generic, and arise small size [150]. This is an area where poly-
when the doubling is not smaller than both atomic molecules, specifically asymmetric top
the fine (e.g. spin-rotation) and hyperfine en- molecules, are a requirement, since a molecule
ergy scales in the rotational state. This is not needs at least 4 atoms to have a handedness at
too difficult to satisfy, especially since the dou- all. A symmetric top with a CH3 group (e.g.
bling scales with rotational number. This de- CaOCH3 ) can be turned into a chiral molecule
pendence on rotational state gives additional by substituting for example CHDT, and such
levels of control over where the crossing occur, molecules offer the possibility of laser cooling
and offers the opportunity to measure the ef- as well [21, 45, 151]. The recent demonstra-
fect at several different crossings for additional tion of laser-cooled CaOCH3 [63] is an impor-
robustness. Furthermore, the 2 Σ electronic tant step toward potentially realizing sensitive
states in these molecules retain the intrinsic measurements in ultracold chiral molecules.
sensitivity of their diatomic counterparts [148]
and are also amenable to laser cooling. SincePolyatomic Molecules as Quantum Sensors for Fundamental Physics 15
5. New forces and fields and refer the reader to reviews for more in-
formation about the very wide variety of other
The nature of dark matter and dark energy, approaches and motivation [1, 153, 154, 155].
which together make up most of the uni- Variations of α and µ are particularly rel-
verse [152], is not understood. This motivates evant for atomic and molecular spectroscopy.
the existence of even more new fields and forces µ dictates the masses of the interacting bodies
which can couple to the Standard Model, and (including the nuclei, which are determined by
frequently give rise to observables to which mp and the neutron mass mn ≈ mp ), and α
atoms and molecules are sensitive [1, 153, 154, sets the strength of the electromagnetic force,
155]. Here we shall consider two cases – fields both of which are responsible for essentially
which change “slowly,” resulting in drifts of all spectroscopic features. For some frequency
fundamental constants, or fields which oscil- splitting ν between two states which depends
late on laboratory timescales, resulting in os- on α and µ, it is common to define the change
cillations of fundamental constants or inducing ∆ν resulting from changes ∆α and ∆µ by
transitions in atoms or molecules. ∆ν ∆α ∆µ
= Kα + Kµ ,
ν α µ
5.1. Variation of fundamental constants where the K parameters are called sensitivity
Despite our ability to precisely measure fun- coefficients. The ν −1 appearing on the left-
damental constants [156] such as the fine- hand side of the equation suggests that the
structure constant α = e2 /(4π0 ~c) = sensitivity parameters are enhanced for nearly-
1/137.035999084(21) and the proton-electron degenerate states, which is indeed frequently
mass ratio µ = mp /me = 1836.15267343(11), the case [153, 154, 159, 160]. This is because
one may wonder whether they are actually we are defining the sensitivity parameters
constants at all. The question is intrinsically as a fractional change in the frequency
interesting, but it also has specific motiva- splitting, though we must be mindful that the
tion [1, 153, 154, 155] as these effects arise experimental frequencies and resolutions are
quite frequently in extensions of the Standard also relevant [160].
Model or General Relativity. For example, Electronic transition energies are ∝
a new field to explain dark energy can re- α µr c2 where µr is the reduced electron-
2
sult in a change of α in order to preserve en- nucleus mass. Since µr ∼ me + O(µ−1 ),
ergy conservation [157], or massive dark matter the sensitivity to µ variation is suppressed by
fields can couple to Standard Model parame- µ−1 ∼ 10−3 , making electronic transitions sen-
ters and result in drifts in coupling constants sitive almost exclusively to α. Transitions in
and masses [158]. Comparison of precise, lab- optical clocks are therefore sensitive probes for
oratory measurements of these quantities over ∆α, and comparing two different optical fre-
human timescales, as well as comparisons of quencies at different times can be used to con-
less precise measurements but over longer cos- strain α̇/α [161]. Microwave clocks relying on
mological or geological timescales, yield very hyperfine structure are sensitive to both α and
strong constraints on such drifts. We will fo- µ since the nuclear magnetic moment depends
cus on laboratory measurements where poly- on mp , while the overlap of the electronic wave-
atomic molecules could make improvements, function depends on me and α. They can
therefore be used to probe both ∆α and ∆µ,Polyatomic Molecules as Quantum Sensors for Fundamental Physics 16
which can be combined with ∆α measurements
from optical clocks to place limits on both α̇/α
and µ̇/µ at the . 10−16 level [162, 163, 164].
While atomic frequency measurements are Small���
currently the most sensitive, molecules have a
Large ��
number of advantages. First, they offer the
opportunity to probe variations in µ directly,
for example through rotational (∝ µ−1 ) or
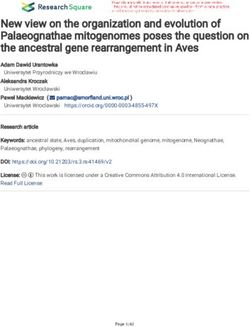
vibrational (∝ µ−1/2 ) constants. Second, Figure 7. An example of an accidental near-
their complex internal structure gives rise to a degeneracy in a molecule [165, 166]. Two vibrational
levels in different potential energy surfaces have a small
wide range of dependencies and energy scales,
energy splitting and different dependence on ωv ∝
and including many “near-degeneracies” which µ−1/2 , and therefore a large enhancement factor.
significantly enhance sensitivity coefficients.
As an example, consider a molecule with
two potential energy surfaces (PESs) sharing molecular clocks to probe the changing
the same dissociation asymptote, as shown in vibrational energy splittings directly, without
figure 7 [165]. Since the PESs arises mostly relying on accidental near-degeneracies [1,
from electronic effects (the chemical bond), a 155, 168, 169]. The complex structure
variation of µ can be considered as a change of polyatomic molecules gives them many
in the reduced mass of the oscillating bodies; more opportunities for near-degeneracies and
in other words, the spring in the harmonic large sensitivity coefficients. An example is
oscillator is mostly unchanged, but the mass the linear (l-) isomer of the C3 H molecule
changes, resulting in a vibration frequency in the 2 Π ground electronic state [170].
change ∝ µ−1/2 . If these two PESs have a The vibrational angular momentum ` in the
pair nearly-degenerate vibrational levels, there bending mode interacts with the electronic
can be a significant enhancement in Kµ . These angular momentum to push one of resulting
degeneracies can also arise in other ways, for states down to be just ∼29 cm−1 above the
example from near-cancellations between spin- absolute ground state. There are nearly-
orbit and vibrational intervals [166], and are degenerate rotationally excited states in the
sensitive to variation of fundamental constants ground and vibrating states, leading to
as long as the two states don’t have the same transitions with both Kα and Kµ ∼1,000 as
dependence on them. This approach was the energies of the states depend on both
recently implemented in ultracold KRb on a vibrational and electronic effects.
transition between excited vibrational states The multiple vibrational degrees of free-
in singlet X 1 Σ+ and triplet a3 Σ+ electronic dom provide a more generic source of acci-
ground states with a sensitivity of Kµ ≈ dental degeneracy. An important example of
15, 000 to set a limit of |µ̇/µ| . 10−14 /yr [167] this is SrOH, which has nearly-degenerate vi-
over a ∼1 year timescale. brational levels giving significantly enhanced
We shall focus on the enhancement due sensitivity Kµ & 1, 000 [171]. In particu-
to near-degeneracies, though it is not the only lar, the (200) and (031 0) vibrational modes in
path forward; one other approach is to use the ground X̃ 2 Σ+ electronic state are within
extremely sensitive measurements in diatomic ∼ 1 cm−1 ∼ 30 GHz of each other, and havePolyatomic Molecules as Quantum Sensors for Fundamental Physics 17
rotational transitions spaced by < 200 MHz, restricted to the axion specifically, as a generic
all of which are experimentally convenient mi- pseudoscalar field (or “axion-like particle”)
crowave frequencies. The sensitivity is ad- will lead to many of the same effects.
ditionally enhanced because the different vi- Furthermore, axion and axion-like parti-
brational modes, in particular the harmonic cles are a promising candidate for dark mat-
and anharmonic contributions, have differ- ter. If dark matter is composed of such a field,
ent dependence on µ. SrOH is particularly we can use the local dark matter density to
compelling since it can be laser-cooled and estimate that θ will oscillate with amplitude
trapped, and in fact was the first laser-cooled ∼ 10−19 [175]. This may seem hopelessly small,
polyatomic molecule [49]. This presents an as the limits on θ from the neutron EDM and
opportunity for extremely sensitive searches Hg EDM experiments are around 9 orders of
leveraging long coherence times and large num- magnitude larger. However, a critical feature
bers. of the axion signature is that it oscillates at
a frequency ωa = ma c2 /~ given by the ax-
5.2. Oscillating fields ion mass ma . In addition, the field is quasi-
coherent; bosonic dark matter particles of mass
We have so far focused on either static quanti-
m .15 eV will have overlapping de Broglie
ties like permanent, CP-violating moments, or
wavelengths, and can therefore be described
quasi-static effects such as slowly drifting con-
as a classical, oscillating field [175]. Sensi-
stants. However, many proposed theories add
tive NMR techniques may therefore be used
new fields which couple to the Standard Model
on macroscopic samples with moles of atoms
and result in oscillating effects. In particular,
or molecules, such as in the CASPEr experi-
we consider in this section oscillations whose
ment [177, 178].
periodicity could be observed in the laboratory,
Molecules offer opportunities to search for
yielding different methods of experimental in-
these effects from oscillating CP-violation as
vestigation.
well. Existing molecular EDM data can be
One important example is the axion,
time-resolved to search for oscillating dipole
which was originally proposed [172] as an
moments up to the experimental repetition
explanation of why the strong force appears
rate of ∼ 1 Hz, as was recently performed
to preserve CP. CP is not a symmetry of
for the HfF+ EDM result [179], so further
nature; the weak force has an order unity CP-
improvements in EDM searches will advance
violating phase, yet the CP-violating term θ in
these bounds. Additionally, molecules offer
the strong force is constrained to be θ . 10−10
the opportunity for resonant enhancement if
by neutron and 199 Hg EDM experiments [120,
the energy splitting between states can be
173]. The axion results from promoting θ to
tuned to match the axion field oscillation
a field which oscillates, so that it has finite
frequency [176]. This results in orders-
amplitude but averages away. Since θ leads
of-magnitude increases in spin precession
to nuclear CP-violation in the form of EDMs,
rates, so the availability of many sources of
NSMs, and MQMs, the oscillating axion field
opposite-parity states with large tunability
results in oscillating (and static [174]) CP-
in polyatomic molecules give them some
violation through these channels [147, 175,
compelling advantages.
176]. Note that these conclusions are not
The time-dependent parity violation ofPolyatomic Molecules as Quantum Sensors for Fundamental Physics 18
these fields also gives rise to new observables getting started. Despite being on the scene for
and measurement methods [147, 180]. Similar only a few years, there are many exciting re-
to how these fields will induce oscillating sults and proposals. As the list of species and
CP-violation, they will also induce oscillating techniques continue to grow, so too will the
P-violation, for example through oscillating possibilities of what to do with these increas-
mixing of opposite parity states. This ing complex quantum objects – not just for
mixing can be measured using qualitatively precision measurement, but for the many other
similar techniques to search for static parity applications which benefit from both complex-
violation, and therefore could benefit from ity and control, such as quantum information,
the advantages of polyatomic molecules for simulation, sensing, chemistry, and more.
many of the same reasons. While static
PV effects are enhanced when the states 7. Acknowledgements
are nearly-degenerate, oscillating PV effects
are resonantly enhanced by many orders of Thanks to Ben Augenbraun, Arian Jadbabaie,
magnitude when the energy splitting between Ivan Kozyryev, Eric Norrgard, and Nick
the states is equal to the frequency of Pilgram for thoughts and feedback.
the oscillating field, as shown in figure 6.
The abundance of opposite-parity states of Appendix: Molecular structure
polyatomic molecules with tunable splittings,
combined with opportunities for laser cooling, Here we give a very brief overview of molecular
offer exciting opportunities for future searches structure in heteronuclear diatomic molecules,
over a wide rage of energy scales difficult to in particular the features relevant to the
probe with other methods. experiments discussed. Molecular structure is
Another approach leveraging the large an astoundingly large and complex field, and
span of energy scales in molecules is to we will not even scrape the surface [16, 17, 22,
search for resonant absorption of DM [181, 183].
182]. The coherent, oscillating coupling to the Electronic states of molecules have term
molecular constituents can result in molecular symbols 2S+1 ΛΩ , very analogous to the 2S+1 LJ
excitation, which can then be detected from symbols of atoms. In both cases S denotes
the total electronic spin, while Λ = L ~ · n̂
subsequent spontaneous decay or via state-
specific detection of the excited state. If the and Ω = J~ · n̂ denote the projections of the
electronic orbital angular momentum L ~ and
transition is tuned using the Stark or Zeeman
effect to be resonant with the oscillation total electronic angular momentum J~ onto the
of the field, there will be a resonance in internuclear axis n̂. The strong electrostatic
the absorption rate, yielding a method to forces quantize the orbital angular momentum
~ along the internuclear axis, hence the
L
differentiate the signal from backgrounds.
appearance of Λ in the term symbol. When
written in the term symbol, Λ is denoted by the
6. Outlook
capital Greek versions of the usual atomic term
This entire perspective is an outlook, as re- symbols: Σ, Π, ∆, . . . denote Λ = 0, 1, 2, . . ..
search with laser-cooled polyatomic molecules We also define Σ = S ~ · n̂, so Ω = Λ + Σ.
(and even diatomic molecules) is really just Electronic energy scales are similar to thosePolyatomic Molecules as Quantum Sensors for Fundamental Physics 19
in atoms. imum at an equilibrium distance re , typically
Each electronic state is assigned a letter, a few Å, and a spectrum of vibrational lev-
with X indicating the ground state. The els corresponding to excited states of this po-
traditional labeling scheme is that states with tential. Vibrational frequencies ωv are typi-
the same spin multiplicity as the ground cally in the range of ∼ 100 − 1, 000 cm−1 ,
state are labeled A, B, C, . . ., and those with where the conventional unit cm−1 means fre-
different multiplicity are labeled a, b, c, . . . in quency of c/(1 cm) ≈ 30 GHz or an energy of
order of increasing energy, though there are ≈0.1 meV. Vibrational frequencies are there-
frequent exceptions to this as sometimes states fore in the tens to few hundred THz, or the
are discovered out of order. The state labels near- to mid-infrared. Because the PES is
are usually written with the term symbol, for anharmonic, the lowest few vibrational states
example X 2 Σ+ . The ± superscript in Σ states might have an approximately even spacing, but
indicates the parity of the lowest rotational higher levels rapidly depart from linear spac-
state. This superscript is absent for states ing. Even near the bottom of the potential, the
of higher Λ because, as we shall see, each non-linearities in the energy spacing is usually
rotational state is split into doublets of both tens of GHz or more.
parity in those cases. Each vibrational state has a series of
Spin-orbit coupling splits states with the rotational lines, along with fine and hyperfine
same S and Λ but different Ω, for example features. The energy of a state with J
the 2 Π1/2 and 2 Π3/2 , very similar to alkali rotational quanta is given by BJ(J + 1),
atoms, and with a magnitude and scaling with where the rotational constant B ∝ 1/(µre2 ),
proton number Z. Spin-orbit coupling also where µ is the reduced mass of the nuclei.
mixes states with different Λ and Σ, but the Rotational constants vary from ∼ 100 GHz for
same Ω [184], meaning that Λ and Σ are not a heavy hydride, to ∼ 1 GHz for a heavy-heavy
strictly good quantum numbers (technically, molecule like I2 . Typical molecules used for
Ω isn’t either [184]). However, in the limit laser cooling and for precision measurements
of small spin-orbit coupling, for example in are heavy fluorides or oxides, which have
a molecule with light atoms or arising from rotational constants of ∼ 10 GHz. The
an electronic state with L = Λ = 0, these rotational constant actually depends on the
are reasonably good quantum numbers, and vibrational level, for example because the
will work well for the molecules we consider distance between the molecules changes due to
(even the heavy ones, since we will primarily the skewed character of the PES, but that is
consider Σ states.) The different coupling usually not a significant effect for our purposes.
schemes of all the angular momenta are All heteronuclear molecules have the
described by Hund’s cases, which we will not structure described so far, so further descrip-
consider here, but are of critical importance tion would require additional specification of
to understanding the details of electronic and the molecular details – and rapidly gets very
rotational structure [183]. complicated. We will not need the details of all
Each electronic state has a potential en- these possible interactions, save for one which
ergy surface (PES) indicating the energy of is important to a number of applications dis-
the system as a function of internuclear sep- cussed here.
aration. Bound states posses an energy min- In states with Λ = 0, the ladder ofYou can also read